相关试题
换一换


若正实数x,y满足x+y=xy,则x+4y的最小值是()
A.7 B.8 C.9 D.13
答案
(15)若正实数x,y满足2x+y+6=xy,则xy的最小值是 .
答案
设x,y是实数,则可以确定x3+y3的最小值。(1)xy=1(2)x+y=2
A.条件(1)充分,但条件(2)不充分 B.条件(2)充分,但条件(1)不充分 C.条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分 D.条件(1)充分,条件(2)也充分 E.条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案
已知函数y=x²-4x+3在区间[-1,m]上有最小值-1.则实数m的取值范围是()
答案
若点P(x,y)在直线x+y-4=0上,O为原点,则|OP|的最小值是()
A.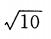 B.
B.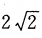 C.
C.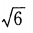 D.2
D.2
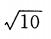 B.
B.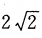 C.
C.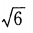 D.2
D.2 答案
求函数z=x2-xy+y2在区域D:|x|+|y|≤1上的最大、最小值。
答案
若x+y=7,xy=10,则x2﹣xy+y2的值为()
A.30 B.39 C.29 D.19
答案
设x⊕y=2x+3y,x⊙y=x•y,且x、y均为正整数,若当x⊙y=6时,x⊕y取得最小值,则x等于:
A.2 B.6 C.4 D.3
答案
求f(x,y)=xy在圆周L:(x-1)2+y2-1=0上的最大值和最小值。
答案
函数y=4sin2x(x∈R)的最小值是( )
A.-4 B.-1 C.0 D.4
答案
热门试题
设x,y都是实数,则x2+y2=0是xy=0的()条件
已知函数y=4/(x-3),当3<x≤4,y的最大值为4,y的最小值为-4。()
已知≤0<2π,且实数x满足log3x=2-cos2θ+sin2θ,则x的最小值是______。
若正数a,满足1/a+1/b=1,则4a+b的最小值是()
若函数f(x)=x2-2bx+3a在区间(0,1)上有最小值,则实数b的取值范围是()
已知直线3x+4y-5=0,x2+y2的最小值是.
设随机变量X、Y有正的方差,若ρXY=0,则( ).
已知y=2∣x-a∣+∣x-2∣的最小值为1,则a=
如果实数x、y满足3x²+4y²=12,那么3x+2y的最大值是()
设 x,y∈R,且 x+y=5,则3x+ 3y的最小值是_____。
求函数f(x,y)=x2+y2在条件x2+y2-xy-1=0下的最大值和最小值。
若函数u=xy·f[(x+y)/xy],f(t)为可微函数,且满足x2∂u/∂x-y2∂u/∂y=G(x,y)u,则G(x,y)必等于( )。
若实值函数F定义域为全体实数,且满足任意x,y:f(z+3)=f(x)f(y)。此时,若f(8)=4,则有f(2)=()
已知直线3x+4y-5=0,x2+y2的最小值是( )。
已知实数x,y,z满足x2+y2+z2-2x+4y-6z+14=0,则x+y+z=()。
函数y=4sin2x+3(x∈R)的最小值和最大值分别是( )
函数y=(x-2)2在区间[0,4]上的最小值是_________.
若直线x-y+m=0与圆x²+y²=1相切,则实数m的值为()
若f(x+y,xy)=2x2+xy+2y2,则f(x,y)=().
当∣x∣≤4时,函数y=∣x-1∣+∣x-2∣+∣x-3∣的最大值与最小值之差是()



 使用微信扫一扫登录
使用微信扫一扫登录