相关试题
换一换


若直线y=x+b与圆x²+y²-2y-1=0相交,则b的取值范围是()
A. B.
B. C.-
C.- D.
D.
 B.
B. C.-
C.- D.
D.
答案
若直线y=x+m与圆x²+y²=1相交,则m的取值范围为()
A.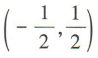 B.(-1,1) C.
B.(-1,1) C.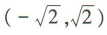 D.
D.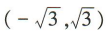
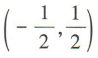 B.(-1,1) C.
B.(-1,1) C.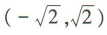 D.
D.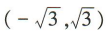
答案
直线y=2x与圆x2+y2=9相交。
A.对 B.错
答案
直线y=x与圆(x-1)2+y2=4相交。
A.对 B.错
答案
若直线x-y+1=0与圆(x-a)²+y²=2有公共点,则实数a的取值范围是()
A.[-3,-1] B.(-3,1) C.[-3,1] D.(-∞,-3)U(-1,+∞)
答案
直线l:3x-y-6=0与圆C:x2+y2-2x-4y=0相交于A,B两点,则|AB|=()
A.10 B.5 C.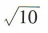 D.
D.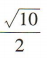
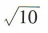 D.
D.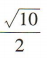
答案
直线x-y+3=0和直线2x=y-1相交。
A.对 B.错
答案
若圆x2+y2=c与直线x+y=1相切,则c=()
A.1/2 B.1 C.2 D.4
答案
已知集合A={x|-1≤x<2},B={y|y≤m},若A∪B=B,则m的取值范围是()
A.{m|m2}
答案
若直线ax-y-2a-1=0与圆x²+y²-2x-1=0相切,则a的值是()
A.2 B. C.1 D.
C.1 D.
 C.1 D.
C.1 D.
答案
热门试题
已知直线y=2x+a与直线y=-x+b相交于点A(-2,0),则a+b=4。
若斜率为√3的直线与y轴交于点A,与圆x²+(y-1)²=1相切于点B,则|AB|=______
过点(0,1)的直线与圆x2+y2=4相交于A,B两点,则|AB|的最小值为()
若直线(x-1) /1= (y+1) 12= (z-1)几与(x+1) /1= (y-1) /1=z/1相交,则必有( )。
若x+y=7,xy=10,则x2﹣xy+y2的值为()
若方程x2+y2+mx-4y+5=0表示圆,则实数m的取值范围是()
若直线mx+4y-2=0与直线2x-5y-12=0垂直,则实数m的取值为()
若直线(m-2)x+y-2=0的倾斜角的范围a∈(90°,180°),则m的取值范围是()
若直线x-y+m=0与圆x²+y²=1相切,则实数m的值为()
已知圆x2+y2-2x+4y=0与直线y=kr+4,问k为何值时,直线与圆相交、相切、相离。
直线x+y+2=0与直线x-y=0相交于点(-1,-1)。
已知直线x-y+1=0,圆(x-1)²+y²=2,则直线与圆的位置关系是()
若直线x+y+2=0与圆x2+y2=m相切,则实数m等于()
若方程x2+y2+6x+m=0表示一个圆,则m的取值范围是()
若直线3x+4y+k=0与圆x2+y2-6x+5=0相切,则k的值等于()
当k为何值时,直线y=kx+2与圆x²+y²=1:
(1)相交;(2)相切;(3)相离.
若点P(1,1)在圆C:x2+y2+x-y+k=0的外部,则实数k的取值范围是()
若直线l:ax+by+1=0平分圆C:x2+y2+2x+2y-1=0,则a+b=()
设直线y=2x+m与抛物线y2=4x没有公共点,则m的取值范围是______。
若f(x+y,xy)=2x2+xy+2y2,则f(x,y)=().



 使用微信扫一扫登录
使用微信扫一扫登录