相关试题
换一换


若函数f(x)=x²+x在区间(a,1-2a)上单调递增,则a的取值范围为()
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
若二次函数y=x²-2ax+1在区间[-2,1]上单调递增,则实数a的取值范围为()
A.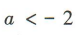 B.
B.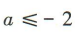 C.
C.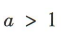 D.
D.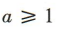
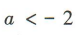 B.
B.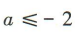 C.
C.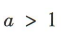 D.
D.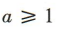
答案
已知函数f(x)是奇函数,且在区间[1,2]上单调递减,则f(x)在区间[-2,-1]上是单调递增函数。()
答案
函数y=x2-2ax 1,若它的增区间是[2, ∞),则a的取值是多少?若它在区间[2, ∞)上递增,则a的取值范围是什么?
答案
若可导函数?(x)在区间I上单调,则其导函数?′(x)也单调。()
答案
若可导函数?(x)在区间I上单调,则其导函数?′(x)也单调()
A.正确 B.错误
答案
若函数y=x²+(2a-1)x+1在区间(-∞,2)上单调递减,则实数a的取值范围是()
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
下列函数中,在区间(0,+∞)上单调递增的是()
A.y=sinx B. C.y=x2 D.
C.y=x2 D.
 C.y=x2 D.
C.y=x2 D.
答案
若f(x)是闭区间[a,b]上单调递增的连续函数,且f(a)f(b)
A.对 B.错
答案
若函数f(x)=x2+2ax+3在区间[-4,6]上是单调函数,则实数a的取值范围()
答案
热门试题
已知定义在实数集R上的偶函数?(x)在区间[0,+∞)上为单调增函数,若?(1)
函数在区间上连续并且可导,若导数小于零,则函数在该区间上单调减少
函数在区间上连续并且可导,若导数为零,则函数在该区间上单调增加
函数y=4sinx+3在[-π,π]上的单调递增区间为()
若二次函数y=x²-2ax+1在区间[-2,1]上单调递减,则实数a的取值范围为()
函数y=xlnx的单调递增区间是______.
若函数y=f(x)在[-1,1]上是单调函数,则使得y=f(sinx)必为单调函数的区间是()
若函数y=f(z)在[a,b]上单调,则使得y=f(x+3)必为单调函数的区间是()
若函数y=f(z)在[a,b]上单调,则使得y=f(x+3)必为单调函数的区间是()。
如果奇函数f(x)在区间[3,7]上单调递增,且f(4)=5,那么函数f(x)在区间[-7,-3]上()
函数y=sin2x的单调递增区间是______.
函数y=4x+3的单调递增区间是()。
函数y=|2x-1|的单调递增区间是()
函数y=x3+1的单调递增区间是()。
已知函数f(x)在区间(-∞,+∞)上单调增加,则使f(x)>f(2)成立的x的取值范围是().
已知二次函数y=x2+ax+1在区间[1,+∞)上为递增函数,则实数a的取值范围是( )
已知(x)在区间(-∞,+∞)内为单调减函数,且(x)>(1),则x的取值范围是().
函数y=4x2的单调递增区间是()
若函数在区间上连续且单调递减,则其反函数在区间上也连续,但是单调性改变./ananas/latex/p/6829/ananas/latex/p/2342/ananas/latex/p/558838/ananas/latex/p/3215208
函数y=1/x在(0,+∞)上单调递增。()



 使用微信扫一扫登录
使用微信扫一扫登录