设F1(x)与F2(x)分别为随机变量X1与X2的分布函数。为使F(x)=aF1(x)-bF2(x)成为某一随机变量的分布函数,则a与b分别是:()
A. a=3/5,b=-2/5
B. a=2/3,b=2/3
C. a=-1/2,b=3/2
D. a=1/2,b=-2/3
查看答案
相关试题
换一换


设F(x)是随机变量X的分布函数,则对()随机变量X,有P{x1 < X < x2}=F(x1) – F(x2)
A.任意 B.连续型 C.离散型 D.个别离散型
答案
设F1(x)与F2(x)分别为随机变量X1与X2的分布函数。为使F(x)=aF1(x)-bF2(x)成为某一随机变量的分布函数,则a与b分别是:()
A.a=3/5,b=-2/5 B.a=2/3,b=2/3 C.a=-1/2,b=3/2 D.a=1/2,b=-2/3
答案
设F1(x),F2(x)分别是随机变量X1,X2的分布函数,为使F(x)=aF1(x)-bF2(x)是随机变量X的分布函数,则在下列给定的各组数中应取( )。
A.a=3/5,b=-2/5 B.a=2/3,b=2/3 C.a=-1/2,b=3/2 D.a=1/2,b=-3/2
答案
设F1(x)和F2(x)都是随机变量的分布函数,则为使F(x) = aF1(x) – bF2(x)成为随机变量的分布函数,系数a和b必须满足()
A.a = 2/3, b = – 2/3 B.a = 3/5, b = – 2/5 C.a = – 1/2, b = 3/2 D.a = 1/2, b = – 3/2
答案
中国大学MOOC: 设有n维随机变量(X1,X2,…,Xn),其分布函数是指F(x1,x2,…,xn) =P{X1£x1,X2£x2,…,Xn£xn},其中x1,x2,…,xn,为任意实数.
答案
设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().
A.F(z)=F(-x) B.F(x)=F(-x) C.F(X)=F(-x) D.f(x)=f(-x)
答案
设随机变量X的分布函数为F(x),则Y=2X+1的分布函数为()。
A.(0 B.(2y+1) C.2F(y)+1 D.0
答案
设随机变量X的分布函数为F(x),则Y=2X+1的分布函数为()。
A.G(y)=2F(y)+1 B.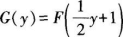 C.
C.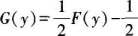 D.
D.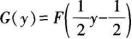
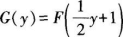 C.
C.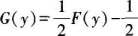 D.
D.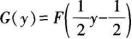
答案
设F1(x)和F2(x)都是随机变量的分布函数,在下列a和b的各对取值中,能够使得F(x)=aF1(x) - bF2(x)成为某个随机变量的分布函数的是.
答案
中国大学MOOC: 函数 F(x)=1/x2可以作为某随机变量的分布函数.
答案
热门试题
X1和X2是任意两个相互独立的连续型随机变量,它们的概率密度分别为f1(x)和f2(x),分布函数分别为F1(x)和F2(x),则( )。
X1和X2是任意两个相互独立的连续型随机变量,它们的概率密度分别为f1(x)和f2(x),分布函数分别为F1(x)和F2(x),则( ).
设X1,X2,Y均为随机变量,已知Cov(X1,Y)=-1,Cov(X2,Y)=3,则Cov(X1+2X2, Y)=________.
设F(x)是随机变量X的分布函数,则对()随机变量X,有P{X₁
如果X的分布函数为F(x), 则对任意实数x1 < x2 ,有P{ x1 < x2 }=F(x2) – F(x1)()
设随机变量X的概率密度函数为f(X)=1/2√∏e
随机变量X在区间(-1,2)上均匀分布,F(x)是X的分布函数,则F(1)=0()
设 f(x) 和 F(x) 分别是随机变量X 的分布密度函数和分布函数,则对任意a
设随机变量X1和X2都服从[0,2]上的均匀分布,则E(X1+X2)=()。
设F(x)为随机变量X的分布函数,则有( )
设随机变量X的密度函数为f(x)=Ae
-|x|,-∞<x<+∞,F(x)是X的分布函数,则有()。
中国大学MOOC: 设F1(x)和F2(x)都是随机变量的分布函数,f1(x),f2(x)是相应的概率密度,则( ).
设函数f(x)在(a,b)内连续,a<x1<x2<…<xn<b,证明:必∃ξ∈(a,b),使f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。
设随机变量X1,X2,X3相互独立,其中X1在[0,6]上服从均匀分布,X2~N(0,22),X3服从参数为λ=3的泊松分布,记随机变量Y=X1-2X2+3X3,则D(Y)=____。
设随机变量X的分布函数为F(x),已知F(2)=0.5,F(-3)=0.1,则P{-3
中国大学MOOC: 如果X的分布函数为F(x), 则对任意实数x1 < x2 ,有P{ x1 < X< x2 }=F(x2) – F(x1).
若f(x)、F(x)分别为随机变量X的密度函数、分布函数,则( )。
对于代数系统和, 若存在一个映射f:X→Y,使得对任意x1, x2∈X,有:f(x1*x2)=f(x1)⊙f(x2),f(x1°x2)=f(x1)◎f(x2), 则称f是从到的同态映射,称与同态。
设随机变量X的分布函数为F(x) = P{X ≤ x },则P{X = a }=()
设随机变量X的概率密度与分布函数分别为f(x)与F(x),则下列选项正确的是()



 使用微信扫一扫登录
使用微信扫一扫登录