平均数或数学期望的位置处在概率密度曲线与x轴包围面积的()处。
A. 起点
B. 终点
C. 形心
D. 最大值
查看答案
相关试题
换一换


平均数或数学期望的位置处在概率密度曲线与x轴包围面积的()处。
A.起点 B.终点 C.形心 D.最大值
答案
设(X,Y)的联合概率密度为则数学期望E (XY)等于( )。
A.1/4 B.1/3 C.1/6 D.1/2
答案
设(X,y)的联合概率密度为,则数学期望E(XY)等于()
A.1/4 B.1/3 C.1/6 D.1/2
答案
设随机变量X的概率密度为的数学期望是()
A.3/4 B.1/2 C.2/3 D.1/4
答案
概率密度曲线()
A.位于X轴的上方 B.在X轴上下摆动 C.与X轴之间的面积为1 D.与X轴之间的面积为0
答案
设随机变量x的概率密度为则Y=1/X的数学期望是( )。
A.3/4 B.1/2 C.2/3 D.1/4
答案
已知某个连续型随机变量X的数学期望E(X)=1,则X的概率密度函数不可能是( ).
A.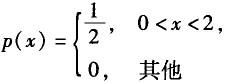 B.
B. C.
C.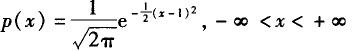 D.
D.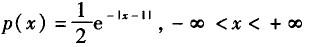
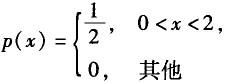 B.
B. C.
C.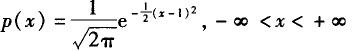 D.
D.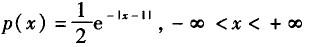
答案
F分布的概率密度曲线是一条对称曲线()
答案
X服从期望为μ,标准差为σ的正态分布,概率密度函数为f(x);期望值μ决定曲线f(x)的“陡峭”或者“扁平”程度()
答案
中国大学MOOC: 由(X,Y)的概率密度f(x,y),可以求Y的边缘概率密度和在X=x时,Y的条件概率密度.
答案
热门试题
正态分布的密度曲线与x轴所围成的面积应等于1。
水文现象中,大洪水出现机会比中、小洪水出现机会小,其概率密度曲线为[ ]。
概率密度函数曲线下的面积等于()。
X服从期望为μ,标准差为σ的正态分布,概率密度函数为f(x);那么f(x)关于直线x=μ对称,且在x=μ处取得最大值()
设随机变量X的概率密度函数f(x)=1/[π(1+x2)],则Y=3X的概率密度函数为( )。
下图是资产组合价值变化ΔΠ的概率密度函数曲线,其中阴影部分表示( )。图 资产组合价值变化ΔΠ的概率密度函数曲线
正态分布曲线从平均数到+∞区域与x轴围成的面积为()
下图是资产组合价值变化ΔΠ的概率密度函数曲线,其中阴影部分表示()。<br/>图资产组合价值变化ΔΠ的概率密度函数曲线
请问在Matlab中下面的哪一个函数可以用来编程计算出信号的概率密度曲线 ?
设随机变量X的概密度为则的数学期望是( )。
设F1(x)与F2(x)为两个分布函数,其相应的概率密度f1(x)与f2(x)是连续函数,则必为概率密度的是
对某工序进行产品质量抽样检验,其样本平均数的数学期望为:20;标准偏差为:1.已知样本量为:4,则本工序产品的平均数和标准偏差为()。
平均寿命E(t)是个箅术平均值,在概率中称()。Ⅰ.数学期望值;Ⅱ.均值
设随机变量X与Y相互独立,已知(X,Y)的概率密度为f(x,y),则随机变量 (-X,-Y)的概率密度为 。(答案请在英文状态下输入)
对于概率密度函数P(x)应强调的是()
位置平均数比数值平均数准确
已知随机变量X的概率密度为,令Y=-2X,则Y的概率密度为/ananas/latex/p/19989/ananas/latex/p/19991
设 X ~ N(0,1),则X的概率密度有性质φ(-x) = φ(x)()
已知连续型随机变量X的概率密度为Φ(X)=
设随机变量X与Y相互独立,已知(X,Y)的概率密度为f



 使用微信扫一扫登录
使用微信扫一扫登录