函数y=4x 在区间(0,+∞)内( )。
A. 是减函数
B. 是增函数
C. 既是增函数又是减函数
D. 既不是增函数也不是减函数
查看答案
相关试题
换一换


函数y=4x 在区间(0,+∞)内( )。
A.是减函数 B.是增函数 C.既是增函数又是减函数 D.既不是增函数也不是减函数
答案
已知函数y=f(x)是R上的偶函数,且在区间(0,+∞)内是减函数,那么它在区间(-∞,0)内( )。
A.是增函数 B.是减函数 C.没有单调性 D.其它三者都有可能
答案
已知函数y=f(x)是R上的奇函数,且在区间(0,+∞)内是减函数,那么它在区间(-∞,0)内是( )。
A.增函数 B.减函数 C.无法判断单调性 D.其它三项都有可能
答案
偶函数y=f(x)在区间[0,4]上单调递减,则有()
A.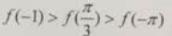 B.
B.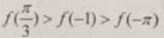 C.
C. D.
D.
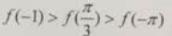 B.
B.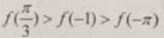 C.
C. D.
D.
答案
正弦函数y=sinx在区间(0,π)内是增函数。
A.对 B.错
答案
函数y=(x-2)2在区间[0,4]上的最小值是_________.
答案
点x=0是函数y=x4的()
A.驻点但非极值点 B.拐点 C.驻点且是拐点 D.驻点且是极值点
答案
点x=0是函数y=x4的
答案
设在区间(-∞,+∞)内函数f(x)>0,且当k为大于0的常数时有f(x+k)=1/f(x)则在区间(-∞,+∞)内函数f(x)是( )。
A.奇函数 B.偶函数 C.周期函数 D.单调函数
答案
已知偶函数y=ƒ(x)在区间[a,b](0
A.增函数 B.减函数 C.不是单调函数 D.常数
答案
热门试题
当a<x<b时,有f′(x)>0,f″(x)<0,则在区间(a,b)内,函数y=f(x)的图形沿x轴正向是()。[2012年真题]
函数y=4x+3的单调递增区间是()。
y=f(x)是方程y″-2y′+4y=0的一个解,若f(x0)>0,f′(x0)=0,则函数f(x)( )。
已知偶函数y=f(x)在区间[a,b](0
已知偶函数y=f(x),在区间[a,b](0
函数y=x+cosx在(0,2π)内()
函数y=x+cosx在(0,2π)内()
函数y=x+cosx在(0,2π)内()
设函数f(x)在区间(0,1)内可导,f’(x)>0,则在(0,1)内f(x)()。
函数y=x2x在区间(0,1]上的最小值为____。
函数y=f(x)在(a,6)内二阶可导,且f′(x)>0,f″(x)<0,则曲线y=f(x)在(a,6)内( ).《》( )
函数y=-x2+4x+1的单调递增区间是()
(2012)当a区间(a,b)内,函数y=f(x)图形沿x轴正向是:()
当a则在区间(a,b)内,函数y = f(x)图形沿x轴正向是()
设f(x)是可导函数,且f′(x)=sin(x+1),f(0)=4,x=g(y)是y=f(x)的反函数,则g′(4)=().
确定函数y=2x4-12x2的单调区间、极值及函数曲线的凸凹性区间和拐点.
函数y=4x2的单调递增区间是()
如果在区间(a,b)内,函数f(x)满足f′(x)>0,f′′(x)
设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=____。
设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)>O,f’(x0)=0,则函数f(x)在点x0().



 使用微信扫一扫登录
使用微信扫一扫登录