相关试题
换一换


已知两点M(-2,5),N(4,-1) ,则直线MN的斜率 ( )
A.1 B.-1 C.0.5 D.-0.5
答案
已知点M(1,-1),N(2,5),则线段MN的中点坐标为()
A.(3,4) B.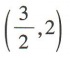 C.(1,6) D.
C.(1,6) D.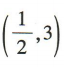
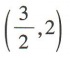 C.(1,6) D.
C.(1,6) D.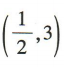
答案
已知点M(-1,5),N(2,1),则线段MN的长为( )。
A.3 B.4 C.5 D.6
答案
已知点M(0,-2)和点N(-3,2),则线段|MN|=( )。
A.3 B.4 C.5 D.6
答案
已知点M(-2,-1),N(-2,4),则线段MN的长为( )。
A.5 B.2 C.4 D.3
答案
已知点M(2,-1),N(2,1),则线段MN的长为( )。
A.-1 B.2 C.1 D.3
答案
已知点M(-3,4),点N(5,2),则线段MN的中点坐标为( )。
A.(4,-1) B.(2,6) C.(1,3) D.(2,3)
答案
已知点M(1,2),N(2,3),则直线MN的斜率为()。
A.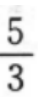 B.1 C.
B.1 C.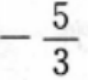 D.-1
D.-1
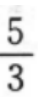 B.1 C.
B.1 C.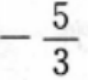 D.-1
D.-1 答案
已知点M(1,2),N(2,3),则直线MN的斜率为()。
A.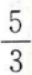 B.1 C.-1 D.
B.1 C.-1 D.
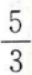 B.1 C.-1 D.
B.1 C.-1 D.
答案
已知2m=3,2n=5,则2m+n的值为()
A.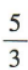 B.2 C.8 D.15
B.2 C.8 D.15
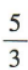 B.2 C.8 D.15
B.2 C.8 D.15 答案
热门试题
已知点M(-3,4)和点N(5,2),则线段MN的中点坐标是( )。
已知点M(2,-4),线段MN的中点坐标是(2,-2),则点N的坐标是( )。
已知点M(0,2),N(-6,-4),则线段MN中点的坐标是()
已知集合M={2,3,5,a},N={1,3,4,b},若M∩N={1,2,3},则a,b的值为()。
已知集合M =(2,3,5,a),N =(1,3,4,b),若M∩N=(1,2,3),则a,b的值为
已知点M(2,1),N(4,3),则线段MN中点的坐标为()
已知集合M={0,1,2,3},N={0,2,4,5},则M∩N=()
已知点M(4,3)和点N(2,7),则线段MN的中点坐标是( )。
已知点M(0,-2),N(-2,2),线段MN的中点坐标为(-1,1)。
已知随机变量X~B(n,1/2),且P{X=5}=1/32,则n=___________
已知m,n∈R,则“m≠0且n≠0”是“mn≠0”的()条件。
已知点M(-3,4)和点(5,2),则线段MN的中点坐标是()
定义:intm=5,n=3;则表达式m/=n+4的值是(),表达式m=(m=1,n=2,n-m)的值是(),表达式m+=m-=(m=1)*(n=2)的值是()-2。
已知集合M={0,1,2},N={1,2},则M∪N=()
已知集合,M={2,3,4},N={2,4,6,8},则M∩N=( )。
已知集合M={2,3,4},N={2,4,6,8},则M∩N=().
设M和N为正整数,且 M>2 ,N>2,MN<2(M+N),满足上述条件的例(M,N)共有()对
设M和N为正整数,且M>2,N>2,MN<2(M+N),满足上述条件的例(M,N)共有()对。
设M和N为正整数,且 M>2 ,N>2,MN<2(M+N),满足上述条件的例(M,N)共有( )对。
若∣m+2∣+(n-1)2=0,则m+2n的值为( ).



 使用微信扫一扫登录
使用微信扫一扫登录