已知函数f(x)=Inx+ax+bx(其中ab为常数且a≠0)在x=1处取得极值。(1)当a=1时,求f(x)的单调区间;
查看答案
相关试题
换一换


已知函数f(x)=Inx+ax+bx(其中ab为常数且a≠0)在x=1处取得极值。(1)当a=1时,求f(x)的单调区间;
答案
已知函数f(x)=5x+bcosx,其中b为常数。那么“b=0”是“f(x)为奇函数”的( )。
A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
答案
设函数f(x)对任意x均满足f(x+1)=af(x),且f′(0)=b,其中a,b为非零常数,则()
A.f(x)在x=1处不可导 B.f(x)在x=1处可导,且f′(1)=a C.f(x)在x=1处可导,且f′(1)=b D.f(x)在x=1处可导,且f′(1)=ab
答案
设在区间(-∞,+∞)内函数f(x)>0,且当k为大于0的常数时有f(x+k)=1/f(x)则在区间(-∞,+∞)内函数f(x)是( )。
A.奇函数 B.偶函数 C.周期函数 D.单调函数
答案
设?(x)是 R 上的可导函数,且?(x)>0。 (1)求 ln?(x)的导函数;(4 分) (2)已知?′(x)-3x2?(x)=0,且?(0)=1,求?(x)。(6 分)
答案
设α、β均为非零常数,已知f(x+x0)=αf(x)恒成立,且f′(0)=β,则f(x)在x0处( )
A.f′(x0)=αβ B.f′(x0)=α C.f′(x0)=β D.不可导
答案
设f(x)是R上的可导函数,且f(x)>0。(1)求lnf(x)的导函数;
(2)已知f,(x)-3x2f(x)=0,且f(0)=1,求f(x)。
(2)已知f,(x)-3x2f(x)=0,且f(0)=1,求f(x)。
答案
已知函数y=f(x)是R上的偶函数,且在区间(0,+∞)内是减函数,那么它在区间(-∞,0)内( )。
A.是增函数 B.是减函数 C.没有单调性 D.其它三者都有可能
答案
已知f(x)是偶函数,且x≥0时,f(r)=3x,则f(-2)=()
答案
已知x→0时,f(x)是无穷小量,且f(x)≠0,则下列函数在x→0时为无穷大量的是()
A.2f(x) B.f(x)+a(a为常数) C.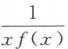 D.f(x2)
D.f(x2)
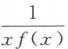 D.f(x2)
D.f(x2) 答案
热门试题
已知函数y=f(x)是R上的奇函数,且在区间(0,+∞)内是减函数,那么它在区间(-∞,0)内是( )。
设F1(x),F2(x)都是分布函数,a>0,b>0是两个常数,且a+b=1。试证明:F(x)=aF1(x)+bF2(x)也是分布函数。
已知偶函数f(x)在[-1,0]上是增函数,且最大值为5,那么f(x)在[0,1]上是( ).
已知函数f(x)=sinx,x<和=0 ,x不等于0,x>0,则f(0)=().
已知函数f(x)的定义域为(-∞,+∞),对任意的x,y,有f(x+y))+f(x-y)=2f(x)f(y)成立,且f(0)≠0.求证:
(1)f(0)=1;
(2)函数f(x)是偶函数.
设函数z=z(x,y)由方程F(y/x,z/x)=0确定,其中F为可微函数,且F2′≠0,则x·(?z/?x)+y·(?z/?y)=( )。
若f (x)的某个原函数为常数,则f (x)=0.
已知f(x)是二次函数,若f(0)=0,且f(x+1)=f(x)+x+1,试求f(x)的解析式.
若f(x)是奇函数且f′(0)存在,则x=0是函数F(x)=f(x)/x的( )。
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f(x)>0,f(x)>0,则在(-∞,0)内必有( )。
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f"(x)>0, f""(x)>0,则在(-∞,0)内必有:
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0,f"(x)>0,则在(-∞,0)内必有()。
设函数f(x)在x=0可导且f(0)=1,又设f(x)满足函数方程f(x+1)=2f(x),求f′(n),其中n是整数。
已知a>0,且a≠1,则函数y=x+a与y=logax的图象可能是()
已知函数f(x)在x0处有二阶导数,且f’(x0)=0,f”(x0)=1,,则下列结论正确的是()。
已知定义域为R的偶函数f(x)在(-∞,0)上单调递减,且f(2)=0,则满足f(x)≥0的x的取值范围是()
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界。已知函数f(x)=l+x+ax2。 (1)当a=-1时,求函数f(x)在(-∞,0)上的值域,判断函数f(x)在(-∞,0)上是否为有界函数,并说明理由; (2)若函数f(x)在x∈[1,4]上是以3为上界的有界函数,求实数a的取值范围。
已知函数y=f(x)对一切x满足,若f’(x0)=0(x0≠0),则().
(2008)设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f′(x)>0,f″(x)>0则在(-∞,0)内必有:()
设函数ψ(x)具有二阶连续导数,且ψ(0)=ψ′(0)=0,并已知yψ(x)dx+[sinx-ψ′(x)]dy=0是一个全微分方程,则ψ(x)等于( )。



 使用微信扫一扫登录
使用微信扫一扫登录