设(a(→)×b(→))·c(→)=2,则[(a(→)+b(→))×(b(→)+c(→))]·(c(→)+a(→))=____。
查看答案
相关试题
换一换


灭火器铭牌上的MF/ABC2表示()
A.2kgABC干粉灭火器 B.2kgAB干粉灭火器 C.20kgABC干粉灭火器
答案
设ABC为三个事件,则ABC同时发生可表为()。
A.A∩B∩Cbr/> B.A∪B∪ C.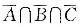 D.
D.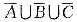
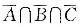 D.
D.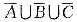
答案
设A(1,2,3),B(-1,2,0),C(1,1,1)则AB(→)·BC(→)=____,AB(→)×BC(→)=____,△ABC的面积=____。
答案
根据下面的购物篮,假定支持度阈值为40%,其中()是频繁闭项集。 TID 项1 abc2 abcd3 bce4 acde5 de
A.abc B.ad C.cd D.de
答案
设字符串变量str1=“abc”; str=2“defg”; 则str1.compareTo(str2)的返回值为()。
A.2 B.-3 C.3 D.-2
答案
已知△ABC中,∠A:∠B:∠C=2:3:5,则△ABC是()
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定三角形的形状
答案
设△ABC的内角A,B,C的对边分别为a,b,c,4a=3b,B=2A,则cosA=()
答案
在△ABC中,2sinBsinC=1+cosA,则△ABC是( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
答案
设△ABC的内角A,B,C的对边分别为a,b,c,已知4a=3b,B=2A,则cosA=()
答案
在△ABC中,a=2,b=3,c=135°,则△ABC的面积等于().
A.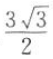 B.
B.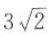 C.
C.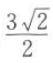 D.3
D.3
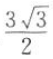 B.
B.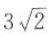 C.
C.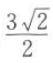 D.3
D.3 答案
热门试题
设某关系模式R(ABC),函数依赖{A→B,B→A,A→C},则R最高满足()
如b2>a2+c2,则△ABC为()
在△ABC中,若lgsinA-lgsinB-lgcosC=lg2,则△ABC是()。
在直角△ABC中,∠A=90°,AB=2,AC=3,则∠ABC的面积等于_____
在△ABC中,若lgsinA-lgsinB-lgcos=lg2,则△ABC是()
编写一汇编语言程序:将字节存储单元BUF中两个压缩BCD码(XYH)拆成两个非压缩BCD码,并转换成两个对应的ASCII码,分别存放在ABC1和ABC2单元中.
在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是()。
设X="ABC",Y="ABCD",则下列表达式中值为.T.的是()。
在△ABC中,∠A=60°,∠C=2∠B,则∠C=()
设则f (π/2)等于()
设tanθ=2,则tan(θ+π)
设tanθ=2,则tan(θ+π)=
ABC的边长分别为a,b,c,则?ABC为直角三角形(1)(c2-a2-b2)(a2-b2)?0(2)?ABC的面积为?ab
在△ABC中,若b=2√2,c=√6+√2,∠B=45°,则a等于()。
已知∆ABC内,AB=2,BC=4,∠ABC=45°,BC在a内,且∆ABC所在平面与平面a成30°,则∆ABC在a内射影的面积是()
设正整数a,b,c,满足a
设n阶方阵A,则|2A|=2|A|.
设ƒ(tanx)=tan2x,则ƒ(2)=()。
设a>b,则-2a( )-2b
设则S (-5/2)等于( )。



 使用微信扫一扫登录
使用微信扫一扫登录