相关试题
换一换


函数y=log2(x+1)的图像大致是()
A. B.
B.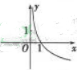 C.
C.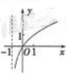 D.
D.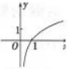
 B.
B. C.
C. D.
D.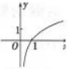
答案
函数f(x)=In|x-1|的图像大致是().
A.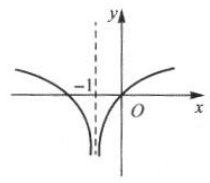 B.
B.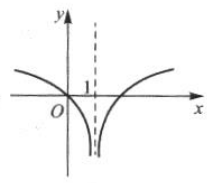 C.
C.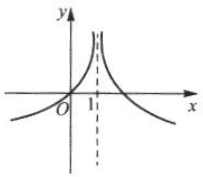 D.
D.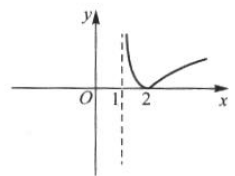
 B.
B. C.
C. D.
D.
答案
函数y=2x的图像大致为( ).
A.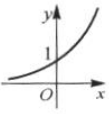 B.
B.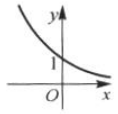 C.
C.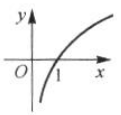 D.
D.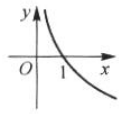
 B.
B. C.
C. D.
D.
答案
一次函数y=2x-3的大致图像为()
A.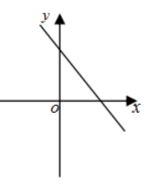 B.
B.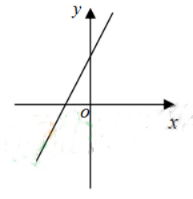 C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
已知函数ƒ(x)=ax2+b的图像经过点(1,2),且其反函数ƒ-1(x)的图像经过点(3,0),则函数ƒ(x)的解析式是( )。
A.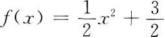 B.ƒ(x)=-x2+3 C.ƒ(x)=3x2+2 D.ƒ(x)=x2+3
B.ƒ(x)=-x2+3 C.ƒ(x)=3x2+2 D.ƒ(x)=x2+3
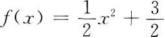 B.ƒ(x)=-x2+3 C.ƒ(x)=3x2+2 D.ƒ(x)=x2+3
B.ƒ(x)=-x2+3 C.ƒ(x)=3x2+2 D.ƒ(x)=x2+3 答案
函数y=x2+1(x>0)的图像在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案
函数y=2x的图像与函数x=log2y的图像( )
A.关于x轴对称 B.关于y轴对称 C.关于直线y=x对称 D.是同一条曲线
答案
已知函数f(x)=(x-m)2+2.
(1)若函数f(x)的图像过点(2,2),求函数y=f(x)的单调递增区间;
(2)若函数f(x)是偶函数,求m的值
答案
点M(1,-1)在函数y=1-2x的图像上.
答案
函数:y=log2(x+2)的图像向上平移1个单位后,所得图像对应的函数为()。
A.y=log2(x+1) B.y=log2(x+3) C.y=log2(x+2)-1 D.y=log2(x+2)+1
答案
热门试题
已知f(x)=ax2+b的图像经过点(1,2)且其反函数f-1(x)图像经过点(3,0),则函数f(x)的解析式是()。
若函数f(x)=log2(5x+1),则其反函数y=f-1(x)的图像过点( )
已知函数f(x+1)的图像过点(3,2),那么与函数f(x)的图像关于x轴对称的图形一定过点()
在一次函数y=2x-1图像上的点是()
已知函数f(x)=ax+b的图像过点(1,3),它的反函数f-1(x)的图像过点(2,0)。试确定f(x)的解析式。
函数y=2sinx在区间[-π,π]上的大致图像为()
要得到函数y=sin2x的图像,只需将函数y=cos2x的图像上的所有点沿x轴()
把函数 的图像变换为函数y=3sin2x的图像需要()
在函数f(x)=2x-5图像上的点是().
将函数y=cosx的图像沿x轴方向向左平移1个单位,便得到函数y=cos(x+1)的图像。()
函数f(x)=log0.5(x+1)的图象大致是()
若把函数y=2(x+3)2+1的图像平移变换成y=2x2的图像,则平移向量a为
下列各点不在函数 f(x)=x+1 图像上的是( )。
已知函数f(x)=ax3-2x的图像过点(-1,4)则a=()
把函数y=x2的图像F平移a=(2,-1),得到F',那么F'对应的函数解析式为________.
设y=(x3+4)/x2。 (1)求函数y的单调区间及极值; (2)求函数图像的凹凸区间及拐点; (3)求函数图像的渐近线; (4)作出函数的图形。
已知一次函数y=2x+b的图像经过点(-2,1),则该图像也经过点( )
已知一次函数y-2x+b的图像经过点(-2,1),则该图像也经过点 ( )
函数:y=x2-2x-3的图像与直线y=x+1交于A,B两点,则|AB|=()。
函数:y=x2-2x-3的图像与直线y=x+1交于A,B两点,则|AB|=()。



 使用微信扫一扫登录
使用微信扫一扫登录