在△ABC中,已知∠A=3∠C=54°,则∠B的度数是()
A. 90°
B. 94°
C. 98°
D. 108°
查看答案
相关试题
换一换


在△ABC中,已知∠A=3∠C=54°,则∠B的度数是()
A.90° B.94° C.98° D.108°
答案
已知△ABC中,∠A:∠B:∠C=2:3:5,则△ABC是()
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定三角形的形状
答案
已知△ABC中,∠A,∠B,∠C所对边为a,b,c,C=30°,a=c=2,则b=____.
答案
已知△ABC中,A:B:C=1:2:3,那么a:b:c为( )
A.1:2:3 B.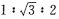 C.3:2:1 D.
C.3:2:1 D.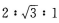
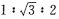 C.3:2:1 D.
C.3:2:1 D.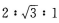
答案
已知△ABC内角A,B,C所对的边分别为a,b,c,若a=3,b=2,A=60°,则cos B=().
答案
已知点A(1,-3),B(0,-3),C(2,2),则△ABC的面积为()
A.2 B.3 C.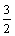 D.
D.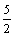
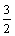 D.
D.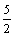
答案
已知点A(1,-3),B(0,-3),C(2,2),则△ABC的面积为()
A.2 B.3 C. D.
D.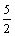
 D.
D.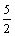
答案
在△ABC中,已知a=4,b=5,c=7,则△ABC是()三角形.
答案
在△ABC中,a=2,b=3,c=135°,则△ABC的面积等于().
A.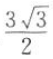 B.
B.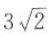 C.
C.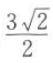 D.3
D.3
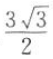 B.
B.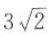 C.
C.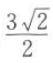 D.3
D.3 答案
设△ABC的内角A,B,C的对边分别为a,b,c,已知4a=3b,B=2A,则cosA=()
答案
热门试题
在△ABC中,已知2B=A+C,b2=ac,则B-A=()。
有a、b、c三个数,已知a×b=24,a×c=36,b×c=54。则a+b+c=( )。
已知△ABC的内角A,B,C的对边分别为a,b,c,且a²=c²-b²+ab,则角C=()
已知在Rt△ABC中,a,b分别为∠A与∠B的对边,∠c=90°,b=8,∠A=15°,则a=()。
出头教育: 已知n阶可逆矩阵A、B、C满足ABC=E,则C=
在Rt△ABC中,∠C=90°,若sinA=1/2,则∠A的度数是()
已知三角形的三边a,b,c满足(b﹣a)(b²+c²)=ba²﹣a³,则△ABC是()
已知点A(1,3),B(2,4),C(-2,6),则判断△ABC的形状.
已知△ABC的内角A,B,C的对边分别为a,b,c,且a²=b²-c²-√2ac,则角B=()
在△ABC中,内角A,B,C的对边分别为a,b,c,若sinA:sinB=2:3,则a:b=()
在△ABC中,∠A=60°,∠C=2∠B,则∠C=()
在△ABC中,内角A,B,C的对边分别为a,b,c,若B=120°,a=3,c=5,则b的值为()
在△ABC中,内角A,B,C的对边分别为a,b,c,若a:b:c=3:2:4,则cosC的值为()
已知三点A(1,2,3),B(3,4,5),C(2,4,7),则△ABC的面积为()。
记△ABC的内角A,B,C的对边分别为a,b,c,面积为√3,B=60°,a²+c²=3ac,则b=
已知△ABC的面积为64,且c与b的等比中项为12,则sinA=______。
已知a=(-1,3),b=(-2,3),c=(0,-1),则(a·b)·c=()。
已知点A(1,2),B(2,3),C(-2,5),那么△ABC是()
在△ABC 中,已知:A(2,2),B(5,6)且 S△ABC=3,求顶点C的轨迹方程.
如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是()



 使用微信扫一扫登录
使用微信扫一扫登录