设M为3×3实数矩阵,a为M的实特征值λ的特征向量,则下列叙述正确的是( )。
A. 当λ≠0时,Ma垂直于a
B. 当λ>0时,Ma与a方向相反
C. 当λ<0时,Ma与a方向相反
D. 向量Ma与a共线
查看答案
相关试题
换一换


设M为3×3实数矩阵,a为M的实特征值λ的特征向量,则下列叙述正确的是( )。
A.当λ≠0时,Ma垂直于a B.当λ>0时,Ma与a方向相反 C.当λ<0时,Ma与a方向相反 D.向量Ma与a共线
答案
设A是3阶矩阵,是A的属于特征值1的特征向量,是A的属于特征值-1的特征向量,则()
A.是A的属于特征值1的特征向量 B.是A的属于特征值1的特征向量 C.是A的属于特征值2的特征向量 D.是A的属于特征值1的特征向量
答案
设A是3阶实对称矩阵,Р是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值入的特征向量,则B的属于特征值A的特征向量是()
A.Pa B.P-1a C.PTa D.(P-1)Ta
答案
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
A.Pa B.P-1A C.PTa D.(P-1)Ta
答案
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
A.Pa B.P-1 C.PTa D.(P-1)Ta
答案
(2009)设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:()
A.Pα B.P-1α C.PTα D.(P-1)Tα
答案
(2009)设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:()
A.Pα B.P-1α C.PTα D.(P-1)Tα
答案
设A是n阶矩阵,λ是A的特征值,其对应的特征向量为X,证明:λ^2是λ^3的特征值,X为特征向量,若A^2有特征值λ,其对应的特征向量为X,X是否一定为A的特征向量?说明理由.
答案
已知二阶实对称矩阵A的特征值是1 , A的对应于特征值1的特征向量为(1, - 1 ) T,若|A|= . -1,则A的另-一个特征值及其对应的特征向量是( )。
A.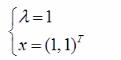 B.
B.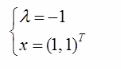 C.
C.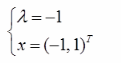 D.
D.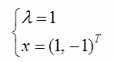
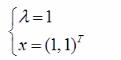 B.
B.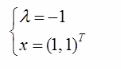 C.
C.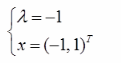 D.
D.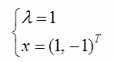
答案
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()
A.α是矩阵-2A的属于特征值-2λ的特征向量 B.α是矩阵的属于特征值的特征向量 C.α是矩阵A*的属于特征值的特征向量 D.α是矩阵AT的属于特征值λ的特征向量
答案
热门试题
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是( )。
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()。
下列命题错误的是: 属于不同特征值的特征向量线性无关|属于同一特征值的特征向量线性相关|特征值相同的矩阵不一定相似|相似矩阵必有相同的特征值
设3阶实对称矩阵A的特征值为-1,1,1,与特征值-1对应的特征向量x=(-1,1,1)′,求A
求解矩阵A的特征值和特征向量的R命令是()
设A是三阶实对称矩阵,r(A)=1,A^2-3A=O,设(1,1,-1)t为A的非零特征值对应的特征向量.(1)求A的特征值;(2)求矩阵A.
设列向量p=[1,-1,2]T是3阶方阵相应特征值λ的特征向量,则特征值λ等于()
若A是实对称矩阵,则A的特征值全为实数()
若A是实对称矩阵,则A的特征值全为实数
设A为n阶方阵,α为A的对应于特征值λ的特征向量,β为AT的对应于特征值μ的特征向量,且λ ≠ μ,证明α与β正交
设A是三阶矩阵,α1=(1,0,1)T,α2=(1,1,0)T是A的属于特征值1的特征向量,α3=(0,1,2)T是A的属于特征值-1的特征向量,则:()
设A是三阶矩阵,α1=(1,0,1)T,α2=(1,1,0)T是A的属于特征值1的特征向量,α3=(0,1,2)T是A的属于特征值-1的特征向量,则:()
设λ1,λ2是矩阵A的两个不同特征值,a,β分别为A对应于λ1,λ2的特征向量,则a,β()
【 】可用来计算矩阵的按模最大的特征值和特征向量
设λ1,λ2是矩阵A的两个不同的特征值,α,β分别为A对应于λ1,λ2的特征向量,则α,β()。
幂法是用来求矩阵(?? )特征值及特征向量的迭代法。
乘幂法主要是用来求矩阵的主特征值(按模最大的特征值)及相应的特征向量。()
A的实特征向量所对应的特征值的绝对值等于1.
若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则( )
中国大学MOOC: 实对称矩阵A的不同特征值对应的特征向量不仅是线性无关的而且是



 使用微信扫一扫登录
使用微信扫一扫登录