设y(x)是区间(0,3/2)内的可导函数,且y(1)=0,点P是曲线L:y=y(x)上的任意一点,L在点P处的切线与y轴相交于点(0,yp),法线与x轴相交于点(xp,0),若xp=yp,求L上点的坐标(x,y)满足的方程。
查看答案
相关试题
换一换


设y(x)是区间(0,3/2)内的可导函数,且y(1)=0,点P是曲线L:y=y(x)上的任意一点,L在点P处的切线与y轴相交于点(0,yp),法线与x轴相交于点(xp,0),若xp=yp,求L上点的坐标(x,y)满足的方程。
答案
设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则曲线y=f(x)在(a,b)内平行于x轴的切线()
A.不存在 B.只有一条 C.至少有一条 D.有两条以上
答案
(2009)设y=f(x)是(a,b)内的可导函数,x △x是(a,b)内的任意两点,则:()
A.△y=f′(x)△x B.在x,x△x之间恰好有一点ξ,使△y=f′(ξ)△x C.在x,x△x之间至少有一点ξ,使△y=f′(ξ)△x D.在x,x△x之间任意一点ξ,使△y=f′(ξ)△x
答案
设y=f(x)是(a,b)内的可导函数,x+△x是(a,b)内的任意两点,则()
A.△y=f′(x)△x B.在x,x+△x之间恰好有一点ξ,使△y=f′(ξ)△x C.在x,x+△x之间至少有一点ξ,使△y=f′(ξ)△x D.在x,x+△x之间任意一点ξ,使△y=f′(ξ)△x
答案
(2009)设y=f(x)是(a,b)内的可导函数,x+△x是(a,b)内的任意两点,则:()
A.△y=f′(x)△x B.在x,x+△x之间恰好有一点ξ,使△y=f′(ξ)△x C.在x,x+△x之间至少有一点ξ,使△y=f′(ξ)△x D.在x,x+△x之间任意一点ξ,使△y=f′(ξ)△x
答案
(2009)设y=f(x)是(a,b)内的可导函数,x+△x是(a,b)内的任意两点,则:()
A.△y=f′(x)△x B.在x,x+△x之间恰好有一点ξ,使△y=f′(ξ)△x C.在x,x+△x之间至少有一点ξ,使△y=f′(ξ)△x D.在x,x+△x之间任意一点ξ,使△y=f′(ξ)△x
答案
设y=f(x)是(a,b)内的可导函数,x,x+△x是(a,b)内的任意两点,则:
A.△y=f’(x)△x B.在x,x+△x之间恰好有一点ξ,使△y=f’(ξ)△x C.在x,x+△x之间至少存在一点ξ,使△y=f’(ξ)△x D.在x,x+△x之间的任意一点ξ,使△y=f’(ξ)△x
答案
设函数y=f(x)在(0,+∞)内有界且可导,则( )。
A.当时,必有 B.当存在时,必有 C.当时,必有 D.当存在时,必有
答案
设函数y=f(x)在(0,+∞)内有界且可导,则( )。
A.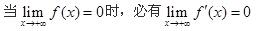 B.
B.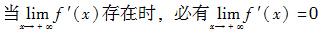 C.
C.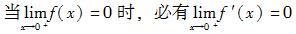 D.
D.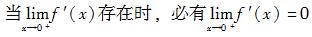
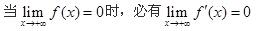 B.
B.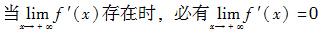 C.
C.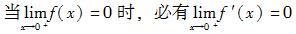 D.
D.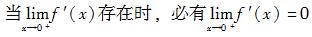
答案
设y=f(x)是(a,b)内的可导函数,x和x+Δx是(a,b)内的任意两点,则:
A.Δy=f" (x)Δx B.在x,x+Δx之间恰好有一点ξ,使Δy=f" (ξ)Δx C.在x,x+Δx之间至少有一点ξ,使Δy=f" (ξ)Δx D.在x,x+Δx之间任意一点ξ,使Δy=f" (ξ)Δx
答案
热门试题
函数y=f(x)在(a,6)内二阶可导,且f′(x)>0,f″(x)<0,则曲线y=f(x)在(a,6)内( ).《》( )
设函数y=f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),曲线f(x)在(a,b)内平行于x轴的切线()。
设函数f(x)在闭区间[a,b]上有定义,在开区间(a,b)内可导,则( )。
若X→Y,且YX,则称X→Y为()/⊂的函数依赖
设函数f(x)可导,且曲线y=f(x)在点(x0,f(x0))处的切线与直线y=2-x垂直,则当Δx→0时,该函数在x=x0处的微分dy是( )。
设f(x)是可导函数,且f′(x)=sin(x+1),f(0)=4,x=g(y)是y=f(x)的反函数,则g′(4)=().
已知函数y=f(x)是R上的偶函数,且在区间(0,+∞)内是减函数,那么它在区间(-∞,0)内( )。
已知函数y=f(x)是R上的奇函数,且在区间(0,+∞)内是减函数,那么它在区间(-∞,0)内是( )。
设函数f(x)和g(x)均在区间[a,b]上连续,在区间(a,b)内可导,且f(a)=f(b)=0,证明:存在一点ξ∈(a,b),使得f’(ξ)+2f(ξ)g(ξ)g’(ξ)=0。
设函数f(x)在区间[-2,2]上可导,且f′(x)>f(x)>0,则( )。
设不恒为常数的函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b)。证明:在(a,b)内至少存在一点ξ,使得f′(ξ)>0。
设函数f(x)在区间[0,2]上连续,在区间(0,2)内可导,且f(0)=f(2)=f(1)=2,证明:至少存在一点ξ∈(0,2),使得f′(ξ)=ξ.
设y=f(3x),其中f(x)为可导函数,则y′=().
设函数y=y(x)是由方程cos(xy)=x+y所确定的隐函数,求函数曲线y=y(x)过点(0,1)的切线方程。
设f(x)是可导函数,且f′(x)=sin2[sin(x+1)],f(0)=4,f(x)的反函数是x=φ(y),则φ′(4)=____。
若函数f(x)在(a,b)内二阶可导,且,则在(a,b)内的函数/ananas/latex/p/267640
设总供给函数AS为Ys=1000+P,总需求函数AD为Yd=1200-P。(1)若总需求曲线向左(平行)移动10%,则均衡点为多少?(2)若总需求曲线向右(平行)移动10%,则均衡点为多少?(3)若总供给曲线向左(平行)移动10%,则均衡点为多少?
设y=f(x)可导,点a0=2为f(x)的极小值点,且f(2)=3,则曲线y=f(x)在点(2,3)处的切线方程为______.
设y=f(x)可导,点a0=2为f(x)的极小值点,且f(2)=3,则曲线y=f(x)在点(2,3)处的切线方程为______
设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=____。



 使用微信扫一扫登录
使用微信扫一扫登录