已知函数y=f(x)是R上的偶函数，且在区间（0，+∞）内是减函数，那么它在区间（-∞，0）内( )。
A. 是增函数
B. 是减函数
C. 没有单调性
D. 其它三者都有可能
查看答案
相关试题
换一换
已知函数y=f(x)是R上的偶函数，且在区间（0，+∞）内是减函数，那么它在区间（-∞，0）内( )。
A.是增函数 B.是减函数 C.没有单调性 D.其它三者都有可能
答案
已知函数y=f(x)是R上的奇函数，且在区间（0，+∞）内是减函数，那么它在区间（-∞，0）内是( )。
A.增函数 B.减函数 C.无法判断单调性 D.其它三项都有可能
答案
已知函数f(x)是定义在R上的偶函数，且在区间[0,+∞)上为减函数，则下列结论正确的是()
A.
B.
C.
D.
B. C. D. 答案
下列函数中为偶函数，且在区间(0，+∞)上是减函数的是（）。
A.y=log3x2 B.y=x2-x C.y=-3｜x｜ D.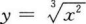
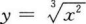
答案
下列函数中，既是偶函数，又在区间（0，3）上为减函数的是 （）
A.y=cosx B.y=log2x C.y=x2-4 D.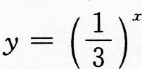
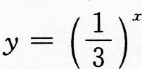
答案
下列函数中，既是偶函数，又在区间(0,3)为减函数的是
A.y=cosx B.y=log2x C.y=x2-4 D.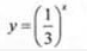
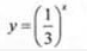
答案
下列函数中，既是偶函数，又在区间（0，3）为减函数的是（）。
A.y=cosx B.y=log2x C.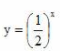
D.y=x2-4
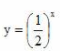D.y=x2-4 答案
已知偶函数y=ƒ(x)在区间[a，b](0
A.增函数 B.减函数 C.不是单调函数 D.常数
答案
如果偶函数f(x)在区间(0,1).上是减函数，且最大值为3，那么f(x)在区间(-1,0)上是()
A.增函数且最大值为3 B.增函数且最小值为3 C.减函数且最大值为3 D.减函数且最小值为3
答案
已知偶函数y=f(x)在区间[a，b](0
A.增函数 B.减函数 C.不是单调函数 D.常数
答案
热门试题
已知偶函数y=f(x),在区间[a,b](0
已知定义域为R的函数f(x)在(8，+∞)上为减函数，且函数y=f(x+8)为偶函数，则( )。
已知定义域为R的函数f（x）在（8，＋∞）上为减函数，且函数y＝f（x＋8）为偶函数，则（ ）。
下列函数中，既是偶函数，又是区间（0,＋∞） 内的增函数是( ).
已知false是定义在R上的偶函数,在false上是减函数,且false,则使false的false的范围是（）
既是偶函数又在区间(0,π)上单调递减的函数是().
下列函数在区间(0，+∞)内是减函数的是( )。
下列函数在区间（-∞，0）内为减函数的是( )。
下列函数在区间（-∞，0）内为减函数的是( )。
下列函数在区间（0，+∞）内为减函数的是( )。
已知定义在实数集R上的偶函数?(x)在区间[0，+∞)上为单调增函数，若?(1)
设函数f(x)在(-∞,+∞)上是偶函数，且在(0,+∞)内有f(x)>0,f(x)>0,则在(-∞,0)内必有（ ）。
设函数f（x）在（-∞，+∞）上是偶函数，且在（0，+∞）内有f＇（x）>0，f＂（x）>0，则在（-∞，0）内必有（）。
设函数f(x)在(-∞，+∞)上是偶函数，且在(0，+∞)内有f"(x)＞0， f""(x)＞0，则在(-∞，0)内必有：
已知偶函数f(x)在[-1,0]上是增函数，且最大值为5，那么f(x)在[0,1]上是( ).
（2008）设函数f（x）在（-∞，+∞）上是偶函数，且在（0，+∞）内有f′（x）>0，f″（x）>0则在（-∞，0）内必有：（）
下列函数中既是偶函数又是（-∞，0）上的增函数的是（）
已知f(x)是偶函数，且x≥0时，f(r)=3x,则f(-2)=（）
已知函数ƒ(x)=ax3-x2+bx+1(a，b∈R)在区间(-∞，0)和(1，+∞)上都是增函数，在(0，1)内是减函数． (Ⅰ)求a，b的值； (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程．
下列函数中，既是偶函数又在(0,+∞)内单调递增的是()
使用微信扫一扫登录
