已知函数ƒ(x)=ax3-x2+bx+1(a,b∈R)在区间(-∞,0)和(1,+∞)上都是增函数,在(0,1)内是减函数. (Ⅰ)求a,b的值; (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程.
查看答案
相关试题
换一换


已知函数ƒ(x)=ax3-x2+bx+1(a,b∈R)在区间(-∞,0)和(1,+∞)上都是增函数,在(0,1)内是减函数. (Ⅰ)求a,b的值; (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程.
答案
已知函数f(x)=ax³+bx+3,且f(-2)=1,则f(2)=()
A.-1 B.3 C.4 D.5
答案
已知f(x)=x2+bx+c,且f(1)=0,f(3)=0,则f(-1)=()
A.2 B.4 C.6 D.8
答案
已知函数f(x)=Inx+ax+bx(其中ab为常数且a≠0)在x=1处取得极值。(1)当a=1时,求f(x)的单调区间;
答案
已知函数f(x)是奇函数,且在区间[1,2]上单调递减,则f(x)在区间[-2,-1]上是单调递增函数。()
答案
若函数f(x)=x2-2bx+3a在区间(0,1)上有最小值,则实数b的取值范围是()
A.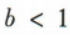 B.
B.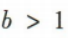 C.
C.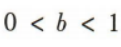 D.
D.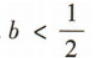
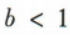 B.
B.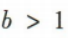 C.
C.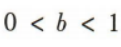 D.
D.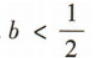
答案
设?(x)是 R 上的可导函数,且?(x)>0。 (1)求 ln?(x)的导函数;(4 分) (2)已知?′(x)-3x2?(x)=0,且?(0)=1,求?(x)。(6 分)
答案
已知函数f(x)=-x2+ax+b的图像关于直线x=2对称,且f(1)=0.
(1)求函数f(x)的解析式;
(2)求函数f(x)在区间[-3,3]上的最小值和最大值.
答案
如果偶函数f(x)在区间(0,1).上是减函数,且最大值为3,那么f(x)在区间(-1,0)上是()
A.增函数且最大值为3 B.增函数且最小值为3 C.减函数且最大值为3 D.减函数且最小值为3
答案
设函数f(x)在闭区间[0,1]上连续,在开区间(0,1)内可导,且f(0)=0,f(1)=1/3,证明:存在ξ∈(0,1/2),η∈(1/2,1),使得f′(ξ)+f′(η)=ξ2+η2。
答案
热门试题
已知奇函数f(x)在区间[1,2]上的最小值为3,最大值为4,则f(x)在区间[-2,-1]上的()
已知函数f(x)=ax³+bx+3满足f(1)=6.则f(-1)=()
已知f(x)在[0,3π/2]上连续,在(0,3π/2)内是函数cosx/(2x-3π)的一个原函数f(0)=0。(Ⅰ)求f(x)在区间[0,3π/2]上的平均值;(Ⅱ)证明f(x)在区间(0,3π/2)内存在唯一零点。
已知二次函数f(x)=ax2+bx+c。则能确定a,b,c的值。(1)曲线y=f(x)经过点(0,0)和点(1,1)。(3)曲线y=f(x)与直线y=a+b相切。
设f(x)是R上的可导函数,且f(x)>0。(1)求lnf(x)的导函数;
(2)已知f,(x)-3x2f(x)=0,且f(0)=1,求f(x)。 已知函数f(x)=ax³+bx(a≠0)满足f(-3)=3,则f(3)=() 已知函数f(x)=2x3-12x+1,求f(x)的单调区间和极值. 已知函数f(x)=2x3-12x+1,求f(x)的单调区间和极值. 已知函数f(x)=x²-2x在区间[0,a]上的最大值与最小值的和为3,则a=() 函数y=x2x在区间(0,1]上的最小值为____。 已知x=-1是函数(x)=ax3+bx2的驻点,且曲线y=(x)过点(1,5),求a,b的值. 函数f(x)=x2+bx+c的图像经过点(-1,0),(3,0),则f(x)的最小值为______。 已知二次函数f(x)=ax2+bx+c,则方程f(x)=0有两个不同实根(1)a+c=0(2)a+b+c=0 已知函数f(x)=(1/2)e2x-ax,g(x)=6xlnx,,h(x)=2e2x-4/x,a>o,b≠0。
(1)求函数f(x)的最小值;(3分)
(2)求函数g(x)的单调区间;(3分)
(3)证明:函数h(x)在[1/2,1]上有且仅有l个零点。(4分) 已知二次函数 f(x)=x2+bx+c的图像过点P(1,0),并且对于任意实数x,有f(1+x)=f(1-x),求函数f(x)的最值。 若函数f(x)=3x2+bx-1(b∈R)是偶函数,则f(-1)=2. 已知函数f(x)=2x3-3x2,求 (1)函数的单调区间; (2)函数f(x)在区间[-3,2]的最大值与最小值。 已知a>0且a≠1,函数f(x)=x²/2,(x>0)
(1)当a=2时,求f(x)单调区间
(2)要使y=f(x)与y=1有有且仅有两个交点,求a取值范围 已知函数f(x)在区间[0,1]上连续,在区间(0,1)内可导,且f(0)=0,f(1)=1,证明: (1)存在一点ξ∈(0,1),使得f(ξ)=1-ξ; (2)存在两个不同的点η,ζ∈(0,1),使得f′(η)f′(ζ)=1. 已知曲线l:y=a+bx-6x2+x3。则(a+b-5)(a-b-5)=0.(1)曲线l过点(1,0)。(2)曲线l过点(-1,0)。
(2)已知f,(x)-3x2f(x)=0,且f(0)=1,求f(x)。 已知函数f(x)=ax³+bx(a≠0)满足f(-3)=3,则f(3)=() 已知函数f(x)=2x3-12x+1,求f(x)的单调区间和极值. 已知函数f(x)=2x3-12x+1,求f(x)的单调区间和极值. 已知函数f(x)=x²-2x在区间[0,a]上的最大值与最小值的和为3,则a=() 函数y=x2x在区间(0,1]上的最小值为____。 已知x=-1是函数(x)=ax3+bx2的驻点,且曲线y=(x)过点(1,5),求a,b的值. 函数f(x)=x2+bx+c的图像经过点(-1,0),(3,0),则f(x)的最小值为______。 已知二次函数f(x)=ax2+bx+c,则方程f(x)=0有两个不同实根(1)a+c=0(2)a+b+c=0 已知函数f(x)=(1/2)e2x-ax,g(x)=6xlnx,,h(x)=2e2x-4/x,a>o,b≠0。
(1)求函数f(x)的最小值;(3分)
(2)求函数g(x)的单调区间;(3分)
(3)证明:函数h(x)在[1/2,1]上有且仅有l个零点。(4分) 已知二次函数 f(x)=x2+bx+c的图像过点P(1,0),并且对于任意实数x,有f(1+x)=f(1-x),求函数f(x)的最值。 若函数f(x)=3x2+bx-1(b∈R)是偶函数,则f(-1)=2. 已知函数f(x)=2x3-3x2,求 (1)函数的单调区间; (2)函数f(x)在区间[-3,2]的最大值与最小值。 已知a>0且a≠1,函数f(x)=x²/2,(x>0)
(1)当a=2时,求f(x)单调区间
(2)要使y=f(x)与y=1有有且仅有两个交点,求a取值范围 已知函数f(x)在区间[0,1]上连续,在区间(0,1)内可导,且f(0)=0,f(1)=1,证明: (1)存在一点ξ∈(0,1),使得f(ξ)=1-ξ; (2)存在两个不同的点η,ζ∈(0,1),使得f′(η)f′(ζ)=1. 已知曲线l:y=a+bx-6x2+x3。则(a+b-5)(a-b-5)=0.(1)曲线l过点(1,0)。(2)曲线l过点(-1,0)。



 使用微信扫一扫登录
使用微信扫一扫登录