设函数f(x),g(x)在[a,b]上连续,且在[a,b]区间积分∫f(x)dx=∫g(x)dx,则()
A. f(x)在[a,b]上恒等于g(x)
B. 在[a,b]上至少有一个使f(x)≡g(x)的子区间
C. 在[a,b]上至少有一点x,使f(x)=g(x)
D. 在[a,b]上不一定存在x,使f(x)=g(x)
查看答案
相关试题
换一换


设函数f(x),g(x)在[a,b]上连续,且在[a,b]区间积分∫f(x)dx=∫g(x)dx,则()
A.f(x)在[a,b]上恒等于g(x) B.在[a,b]上至少有一个使f(x)≡g(x)的子区间 C.在[a,b]上至少有一点x,使f(x)=g(x) D.在[a,b]上不一定存在x,使f(x)=g(x)
答案
设函数f(x)在闭区间[a,b]上积分>0,则f(x)在闭区间[a,b]上
答案
当 在有界区间 上存在多个瑕点时, 在 上的反常积分可以按常见的方式处理:例如,设 是区间 上的连续函数,点 都是瑕点,那么可以任意取定 ,如果反常积分 同时收敛,则反常积分 发散。()
答案
设函数f(x)在[a,b]上连续且f(x)>0,则( )
A.见图A B.见图B C.见图C D.见图D E.见图E
答案
设函数f(x)在[a,b]上连续且f(x)>0,则
A.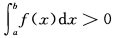 B.
B.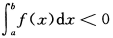 C.
C.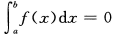 D.
D.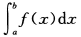 的符号无法确定
的符号无法确定
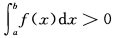 B.
B.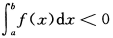 C.
C.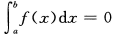 D.
D.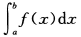 的符号无法确定
的符号无法确定 答案
设函数f(x)在[a,b]上连续且f(x)>0,则()
A.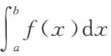 >0 B.
>0 B.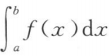 <0 C.
<0 C.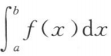 =0 D.
=0 D.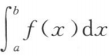 的符号无法确定
的符号无法确定
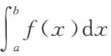 >0 B.
>0 B.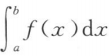 <0 C.
<0 C.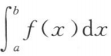 =0 D.
=0 D.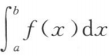 的符号无法确定
的符号无法确定 答案
设函数f(t)在[0,+∞)上连续,
且满足方程,求f(t).
答案
设函数f(x)在区间[a,b]上连续,则下列结论中哪个不正确()?
A.是f(x)的一个原函数 B.是f(x)的一个原函数(a C.是-f(x)的一个原函数(a D.f(x)在[a,b]上是可积的
答案
设函数f(x)在区间[a,b]上连续,则下列结论中哪个不正确?()
A.是f(x)的一个原函数 B.是f(x)的一个原函数 C.是f(x)的一个原函数 D.f(x)在[a,b]上是可积的
答案
设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则曲线y=f(x)在(a,b)内平行于x轴的切线()
A.不存在 B.只有一条 C.至少有一条 D.有两条以上
答案
热门试题
函数 x在区间[0,1]上的定积分是()。
若函数在区间上连续且单调递减,则其反函数在区间上也连续,但是单调性改变./ananas/latex/p/6829/ananas/latex/p/2342/ananas/latex/p/558838/ananas/latex/p/3215208
若f(x)是闭区间[a,b]上单调递增的连续函数,且f(a)f(b)
设函数f(x)在区间[-2,2]上可导,且f′(x)>f(x)>0,则( )。
下列说法正确的有(): 无界函数在闭区间上必定可积|狄义克雷(Dirichlet)函数在闭区间[-1,1]上可积,所以肯定能构造收敛的数值积分公式。|闭区间上有界函数只有有限个间断点,则该函数可积|闭区间上的连续函数必定可积
设函数f(x)和g(x)均在区间[a,b]上连续,在区间(a,b)内可导,且f(a)=f(b)=0,证明:存在一点ξ∈(a,b),使得f’(ξ)+2f(ξ)g(ξ)g’(ξ)=0。
函数在区间上连续并且可导,若导数小于零,则函数在该区间上单调减少
函数在区间上连续并且可导,若导数为零,则函数在该区间上单调增加
函数在区间上连续并且可导,若导数等于零,则函数在该区间是什么函数?
莱布尼兹公式告诉我们:如果函数f(x)在[a,b]上连续,且存在原函数,那么f在区间[a,b]上一定可积。()
设不恒为常数的函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b)。证明:在(a,b)内至少存在一点ξ,使得f′(ξ)>0。
设函数f(x)在区间[0,2]上连续,在区间(0,2)内可导,且f(0)=f(2)=f(1)=2,证明:至少存在一点ξ∈(0,2),使得f′(ξ)=ξ.
函数f(x)在区间[a,b]上连续是它在该区间上可积的( ).
如果函数是在定义区间是连续的,那么其变限积分是可导的。
设f(x)在(-a,a)是连续的偶函数,且当0
设f(x)在(-a,a)是连续的偶函数,且当0()
设f(x)在(-a,a)是连续的偶函数,且当0()
开区间上连续的函数一定有界.
当?(x)在有界区间I上存在多个瑕点时,?(x)在I上的反常积分可以按常见的方式处理。如,可设?(x)是区间[a,b]上的连续函数,点a,b都是瑕点,则可以任意取定c∈(a,b),如果在区间[a,c]和[c,b]上的反常积分同时收敛,那么在区间[a,b]上的反常积分也收敛。
随机变量落在区间(a,b)上的概率为概率密度函数在该区间上的定积分



 使用微信扫一扫登录
使用微信扫一扫登录