已知a=(3,2),b=(2,-1),若(λa+b)∥(a+λb)(λ∈R),求λ的值
查看答案
相关试题
换一换


若已知A∩B=ф,且已知P(A)=0,则()。
A.只有当A=ф,B=ф时,A,B才独立 B.不一定 C.与B独立 D.与B不独立
答案
已知向量a=(2,5),b =(λ,4),若a∥b,则λ=
答案
已知向量a=(4,3),b=(x,4),若a⊥b,则|b|=()
答案
已知直线a,b,平面a,β.若a//a,b//a,则直线a,b的位置关系是().
A.平行 B.相交 C.异面 D.以上均有可能
答案
已知向量a=(1,2),b=(-2,m).若a//b,则a+b=()
A.(-1,-2) B.(-1,2) C.(-3,6) D.(3,-6)
答案
已知集合A={1.2.3},B={a,3.4}.若A∩B={2,3},则a=()
答案
已知向量a=(1,-2),b=(t,1),若a//b,则t=()
A.-1 B.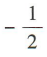 C.
C.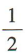 D.1
D.1
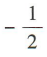 C.
C.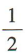 D.1
D.1 答案
● 已知 X = –121,若采用 8 位机器码表示,则[X]原= (21) , [X]补= (22) 。(21)
A.10110111 B.10000111 C.10100111 D.01111001
答案
已知平面向量a=(1,2),b=(x,-4).若a//b,则a▪b=().
A.-6 B.-10 C.0 D.6
答案
已知向量a=(-3,1),b=(x,9),若a⊥b,则x=( )。
A.1 B.2 C.3 D.4
答案
热门试题
已知向量a=(5,1),b=(x,-2),若a⊥b,则x=()
已知向量a=(1,-1),b=(2,x),若a·b=5,则x=()
已知向量a=(2,1),西b=(x,-2),若a∥b,则a+b等于()。
若已知a=10,b=20,则表达式!a
若已知a=20,b=10,则表达式!a>b的值为______。
已知平面向量a=(2,-1),b=(1,x).若a//b,则x=().
已知集合A={1.2},B={a,1},若A∪B={1.2.3}.则实数a的值为()
已知向量a=(k-1,3),b=(k,-4),若a⊥b,则k=()
已知A物体与B物体质量之比为12,体积之比为21,则密度之比 ρAρB= 。
已知a=(3,2),b=(2,-1),若(λa+b)∥(a+λb)(λ∈R),求λ的值
已知向量a=(x,-3),b=(3,1),若a⊥b,则x=-9.
已知函数f(x)=5x+b,若f(-2)=3,则b=()。
已知向量a=(2m,1),b=(1,-3),若a⊥b,则实数m=()
已知向量a=(1,m),b=(2,3).
(1)若a//b,求m的值;
(2)若a⊥b,求3a·(b-3a)的值.
已知2A=3B,B∶C=3∶4,若C比A小2,则B=( )。
● 若信息为32位的二进制编码,至少需要加 (21) 位的校验位才能构成海明码(21)
已知a,b,c,d为实数,若a>b>0,c>d>0,则ac>bd。()
钻孔的质量与钻削余量有关,若钻21~32直径的孔,应留余量为()。
若a,b,c是实数,则能确定a,b,c的最大值.(1)已知a,b,c的平均值.(2)已知a,b,c的最小值.
已知|a|=1,|b|=2。 (1)若a∥b,求a·b; (2)若a、b的夹角为60°,求|a+b|; (3)若a-b与a垂直,求当k为何值时,(ka-b)⊥(a+2b)。



 使用微信扫一扫登录
使用微信扫一扫登录