函数Int(Rnd(0)*10)的取值范围是______。
A. (0,10)
B. (0,1)
C. (1,10)
D. (1,2)
查看答案
相关试题
换一换


函数Int(Rnd(0)*10)的取值范围是______。
A.(0,10) B.(0,1) C.(1,10) D.(1,2)
答案
函数Int(Rnd*6+1)的取值范围是
A.1~7共7个整数 B.0~7共8个整数 C.1~6共6个整数 D.0~6共7个整数
答案
函数AnalogWrite(Pin,i);其中i的取值范围是()
A.0~256 B.1~256 C.0~255 D.0~256
答案
中断函数定义时,中断类型号的取值范围是————
答案
函数Int(Rnd*6+1)的取值范围是______。(1.0分)
答案
若指数函数y=(a+1)x是增函数,则a的取值范围是()
A.(-1,0] B.(-1,0) C.(0,+∞) D.[0,+∞)
答案
如果指数函数y=(a-1)x是减函数,则a的取值范围是().
A. B.
B. C.
C.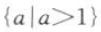 D.
D.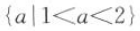
 B.
B. C.
C.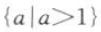 D.
D.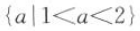
答案
已知函数f(x)=x²-2x+3在[a,3]上的取值范围为[2,6],则实数a的取值范围是()
A.(-0,1] B.[-2,-1] C.[-1,1] D.[-2,1]
答案
指数函数f(x)=(a-1)x在R上是增函数,则a的取值范围是().
答案
函数中根号下x+2中,自变量x的取值范围是()
A.x>-2 B.x≥-2 C.x≠-2 D.x≤-2
答案
热门试题
已知函数f(x)=log(2-a)x是(0,+ ∞)上的增函数,则实数a的取值范围是( ).
函数f(x)=x²+2(a−1)x+2在区间(−∞,4]上是减函数那么实数a的取值范围是( )
消费线性函数中边际消费倾向b的取值范围是什么?
( )是用来衡量随机变量X取值在特定范围内的函数。
若函数f(x)=x²+2(a-1)x+2 在区间(-∞,4]上是减函数,则实数a的取值范围 ( )
函数ROUND(-7.3)的取值是()。
已知(x)在区间(-∞,+∞)内为单调减函数,且(x)>(1),则x的取值范围是().
如果函数f(x)=x2+2(a- 1)x+2在区间(-∞,-4]上是减函数,则a的取值范围是()
已知函数f(x)=x2+(2a-1)x-3
(1)当a=2,x∈[-2,3]时,求函数f(x)的取值范围.
(2)若函数f(x)在[-1,3]上单调递增,求实数a的取值范围.
在函数y=二次根号√(x+4)/x中,自变量x的取值范围是()
若函数f(x)=x2+2ax+3在区间[-4,6]上是单调函数,则实数a的取值范围()
函数f(x)=x2+2(m-1)x+2在区间(-∞,4)上是减函数,则实数m的取值范围是()。
已知函数f(x)在定义域(-1,1)内是减函数,且f(1-a)<f(2a-1),则a的取值范围是()
已知二次函数y=x2+ax+1在区间[1,+∞)上为递增函数,则实数a的取值范围是( )
正相关的取值范围是(),负相关的取值范围是()
控制系统的开环传递函数为,则系统稳定时k的取值范围
水平角的取值范围是( )。竖直角的取值范围是( )
二次函数y=(m-2)2+2x-1中,m的取值范围是()
已知函数f(x)=ax3+3x+2存在极值,求a的取值范围。
已知一次函数y=(4-2m)x+7,若函数y随x的增大而减小,则m的取值范围是()



 使用微信扫一扫登录
使用微信扫一扫登录