通过直观感知、概括归纳出平面向量的基本定理:如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2。请完成下列任务:(1)请设计一个探索该定理的教学过程,并说明设计意图;
(2)请设计一个习题(不必解答),帮助学生进一步巩固该定理,并说明设计意图;
(3)你认为平面向量的基本定理在高中数学课程中占有怎样的地位和作用?
查看答案
相关试题
换一换


通过直观感知、概括归纳出平面向量的基本定理:如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2。请完成下列任务:(1)请设计一个探索该定理的教学过程,并说明设计意图;(2)请设计一个习题(不必解答),帮助学生进一步巩固该定理,并说明设计意图;(3)你认为平面向量的基本定理在高中数学课程中占有怎样的地位和作用?
答案
已知平面向量a,b且满足a▪b=|a|=|b|=2,若e为平面单位向量,则|a▪e+b▪e|的最大值为().
A.3 B.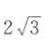 C.4 D.
C.4 D.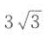
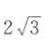 C.4 D.
C.4 D.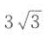
答案
如果→e1,→e2是平面内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基底的是()
A.→e1与→e1+→e2 B.→e1-2→e2与→e1+2→e2 C.→e1+→e2与→e1-→e2 D.→e1-2→e2与-→e1+2→e2
答案
下列属于通过直观感知传递教学内容的方法的有()
A.实验法 B.演示法 C.参观法 D.练习法
答案
学生直观感知的教具有哪些?()
A.感知直观 B.实物直观 C.态度直观 D.模象直观
答案
已知平面向量a=(1,1),b=(1,-1),则两向量的夹角为()。
A. B.
B.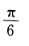 C.
C.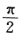 D.
D.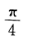
 B.
B.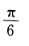 C.
C.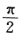 D.
D.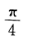
答案
已知平面向量a=(1,1),b=(1,-1),则两向量的夹角为( )
A. B.
B.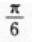 C.
C.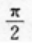 D.
D.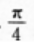
 B.
B.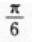 C.
C.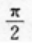 D.
D.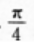
答案
如果进栈序列为e1,e2,e3,e4,则可能的出栈序列是
A.e3,e1,e4,e2 B.e2,e4,e3,e1 C.e3,e4,e1,e2 D.任意顺序
答案
已知e1、e2是两个单位向量,其夹角为60°,试求向量2e1+e2与b=-3e1+2e2的夹角θ
答案
已知平面向量a=(-1,2),b=(1,0),则向量3a+b=().
A.(2.6) B.(-2,-6) C.(-2.6) D.(2,-6)
答案
热门试题
以直观感知为主的教学方法是()。
以直观感知为主的教学方法包括()。
以直观感知为主的教学方法有()
以直观感知为主的教学方法包括()
以直观感知为主的教学方法包括()
通过直观感知、操作确认,归纳出平面与平面平行的判定定理:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行。请完成下列任务:(1)写出本节课的教学目标和教学重点;(2)请设计一个引入新课的问题情境以展开新课的教学,并说明设计意图;(3)请设计一个探索活动来探究该定理;(4)请你设计两道习题(不必解答),进一步帮助学生理解并应用该定理,并说明设计意图。
如果进栈序列为 e1,e2,e3,e4,则不可能的出栈序列是( )。
通过直观感知、操作确认,归纳出直线与平面垂直的判定定理:一个直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。请你完成下列任务:(1)请你设计一个探索该定理的活动或问题情境,并说明设计意图;(2)请你设计一个习题(不必解答),以帮助学生理解该定理,并说明具体的设计意图;(3)请你设计一个习题(不必解答),进一步巩固、应用该定理,并说明具体的设计意图。
通过直观感知、操作确认,归纳出直线与平面垂直的判定定理:一个直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。请你完成下列任务:(1)请你设计一个探索该定理的活动或问题情境,并说明设计意图;(10 分)(2)请你设计一个习题(不必解答),以帮助学生理解该定理,并说明具体的设计意图;(10 分)(3)请你设计一个习题(不必解答),进一步巩固、应用该定理,并说明具体的设计意图。(10 分)
若平面向量a=(x,1),&=(1,-2),且a//b,则x=______.
已知平面向量a=(1,-1),b=(-1,2),则a+b=()
已知平面向量a=(1,t),b=(-1,2),若a+mb平行于向量(-2,1),则
已知平面向量a=(1,t),b=(-1,2),若a+b行于向量(-2,1),则( )
若平面向量a=(x,1),b=(1,-2),且a∥b,则x=________.
若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
已知平面向量a=(2,-1),b=(1,x).若a//b,则x=().
已知平面向量a=(2,1),b=(-1,1),则a+b=
已知平面向量a=(2,1),b=(-1,1),则a+b=().
已知平面向量a=(-2,1)与b=(λ,2)垂直,则λ=()。
已知平面向量a(-2,1)与b= (A,2)垂直,则A=



 使用微信扫一扫登录
使用微信扫一扫登录