已知向量a=(1,2),b=(1,0),c=(3,4),若λ为实数,且(a+λb)//c,则λ=().
A. 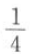 B.
B. 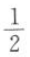 C. 1
D. 2
C. 1
D. 2
查看答案
相关试题
换一换


已知向量a=(1,2),b=(1,0),c=(3,4),若λ为实数,且(a+λb)//c,则λ=().
A.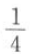 B.
B.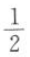 C.1 D.2
C.1 D.2
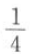 B.
B.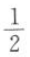 C.1 D.2
C.1 D.2 答案
已知向量a ⃗=(2,8),b ⃗=(4,m),且向量a ⃗平行向量b ⃗,则实数m等于()
A.6 B.10 C.12 D.16
答案
已知向量a=(2m,1),b=(1,-3),若a⊥b,则实数m=()
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
若a,b,c为实数,且a>b,则()
A.a-c>b-c B.a²>b² C.ac>bc D.ac²>bc²
答案
已知a,b,c,d为实数,a>b且c>d,则a-c>b-d()
答案
已知a,b,c,d为实数,若a>b>0,c>d>0,则ac>bd。()
答案
已知向量a=(k,2k)(k>0),b=(3,4),若(a+b)⊥(a-b),则实数k=()
答案
已知a,b,c,d为实数,且c>d,则“a>b”是“a-c>b-d”的( )。
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
答案
已知向量a=(-2,x),b=(y,-1),c=(-4,2),且a⊥b,b//c,则()
A.x=4,y=-2 B.x=4,y=2 C.x=-4,y=-2 D.x=-4,y=2
答案
已知向量a=(k,3),b=(1,4),c=(2,1),R(2a一3b)上c,则实数k=( )。
A.-4.5 B.0 C.3 D.5.5
答案
热门试题
设向量a=(t,-6),b=(-3,2).若a//b,则实数为()
若实数a,b,c满足a∶b∶c=1∶2∶5,且a+b+c=24,则a2+b2+c2=
已知△ABC的面积为64,且c与b的等比中项为12,则sinA=______。
已知向量a=(-2,1),b=(3,-4),且a▪c=-1,b▪c=9,则c的坐标为().
已知平面向量a=(-3,m),b=(m-2,-1),若a与b的方向相反,则实数m的值为()
设 a,b,c 为实数,且 a>b, 则()
设a,b,C为实数,且a>b,则( )
设a,b,c为实数,且a>b,则
设a,b,c为实数,且a>b,则()
已知△ABC的内角A,B,C的对边分别为a,b,c,且a²=c²-b²+ab,则角C=()
已知向量a=(3,1),b=(1,0),c=a+kb.若a⊥c,则k=
已知向量a= (2,3), b=(1,m) ,且 a垂直b,那么实数 m 的值为_____。
已知向量a= (2,3), b=(1,m) ,且 a垂直b,那么实数 m 的值为_____
若实数a>b>c,则ac>bc。()
已知向量a,b满足|a|=7,|b|=12,a·b=-42,则向量a,b的夹角为()
已知△ABC的内角A,B,C的对边分别为a,b,c,且a²=b²-c²-√2ac,则角B=()
若a,b,c为实数,且a≠0.设甲:b2-4ac≥0,乙:ax2+bx+c=0有实数根,则( )
若向量a,b,c满足a||b且a⊥c,则c•(a+2b)=()
已知a>b,若c是任意实数,则下列不等式中总是成立的是()
已知△ABC的内角A,B,C的对边分别为a,b,c,其中c=2,又向量m=(1,cosC),n=(cosC,1),m·n=1.(Ⅰ)若A=45°,求α的值;(Ⅱ)若a+b=4,求△ABC的面积.



 使用微信扫一扫登录
使用微信扫一扫登录