2025年成考高起点每日一练《数学(理)》1月21日

• 1. 教室里有50人在开会，其中学生35人，家长12人，老师3人，若校长站在门外听到有人发言，那么发言人是老师或学生的概率为（）。

  A

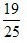
  B

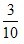
  C

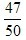
  D

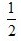
• 2. 若函数f（x）是奇函数，则函数的奇偶性是（）。

  A奇函数

  B偶函数

  C非奇非偶函数

  D即是奇函数，又是偶函数

• 3. 已知两条异面直线m；n，且m在平面α内，n在平面β内，设甲：m//β，n//α；乙：平面α//平面β，则（）。

  A甲为乙的必要但非充分条件

  B甲为乙的充分但非必要条件

  C甲非乙的充分也非必要条件

  D甲为乙的充分必要条件

• 4. 如果不共线的向量a和b有相等的长度,则(a+b)(a-b)=（）  

  A0

  B1

  C-1

  D2

• 1. 在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量关于基底{a,b,c}的分解式 （Ⅱ）求证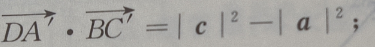： （Ⅲ）求证：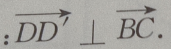  

• 2. 设分别讨论x→0及x→1时f（x）的极限是否存在？

• 3. 已知等差数列｛an｝中，a1+a2+a3=6,a2+a4+a5= 12求｛an｝的首项与公差。  

• 4. 在△ABC中如果sinA=2sinBcosC，求证：△ABC是等腰三角形。  

• 1. ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图 ，设A与B重合后的点为P，则面PCD与面ECD所成的二面角为______度，PE与面ECD成______度。

• 2. 九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。