2023年高职单招每日一练《数学》1月8日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：197
试卷答案：有
试卷介绍： 2023年高职单招每日一练《数学》1月8日专为备考2023年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. 抛物线y2=-8x的焦点坐标是(2,0).
A对
B错
-
2. 不等式x2-5x-6≤0的解集是(x|-2≤x≤3}.
A对
B错
-
1. 已知tan α,tan α是方程
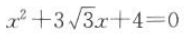的两根，且
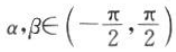,则α+β的值为().A
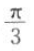
B
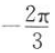
C
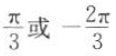
D
-
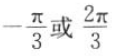
2. 已知平面向量a,b是非零向量，|a|=2,a
(a+2b),则向量b在向量a方向上的投影为().A1
B-1
C2
D-2
-
1. 如图，设F1,F2分别为椭圆
的左、右焦点，且|F1F2|=2√2.(1)求椭圆C的标准方程；
(2)设P为第一象限内位于椭圆C上的一点，过点P和F2的直线交y轴于点Q.若QF1⊥QF2，求线段PQ的长.
-
2. 袋中有除颜色不同外均相同的6个红色球、3个黄色球、4个黑色球、5个绿色球，现从袋中任取一个球，求取到的球不是绿球的概率.
-
1. 若双曲线经过点
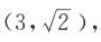,且渐近线方程为
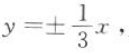,则此双曲线的方程为（）
-
2. 函数
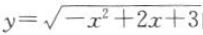的单调增区间是（）.
-
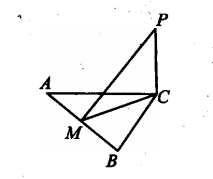
1. 如图∆ABC中，AC=8，∠BAC=60°，PC⊥平面ABC，PC=4，M是AB边上的一个动点，求PM的最小值.
-
2. 已知三个不等式：
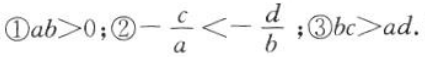以其中两个作为条件，余下一个作为结论，可以组成多少个正确的命题?
相关试卷
相关题库
