初中数学学科知识与教学能力试卷(二)

• 1. 《义务教育数学课程标准(2011年版)》指出，信息技术的发展对数学教育的价值、目标、内容以及教学方式产生了很大影响。下列说法正确的是()。

  A现代信息技术可以完全替代原有的教学手段

  B在应用现代信息技术时，教师不需要课堂教学板书设计

  C现代信息技术真正价值在于实现原有的教学手段难以达到甚至达不到的效果

  D现代信息技术的应用不利于培养学生的几何直观

• 2. 设10≤x1x2x3x4≤104，x5=105，随机变量 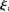取值x1,x2,x3,x4,x5的概率均为0．2，随机变量 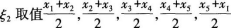的概率也均为0．2。若记 方差，则( )

  A

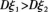
  B

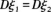
  C

  D 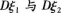的大小关系与x1，x2，x3，x4的取值有关

• 3.
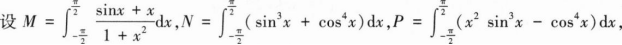
  则有()。

  AM<N<P

  BN

  CM

  DP

• 4.  

  A1

  B-2

  C-1

  D1或-2

• 5. 下列函数在[-1，1]上满足罗尔定理条件的是()。 0.y=ex 1.y=ln|x|2.y=1-x23.

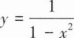
  A-2

  B-1

  C1

  D2

• 6.  

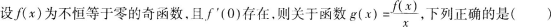
  A在x=0处左极限不存在

  B有跳跃间断点x=0

  C在x=0处右极限不存在

  D有可去间断点x=0

• 7. 发现勾股定理的希腊数学家是( )。

  A泰勒斯

  B毕达哥拉斯

  C欧几里得

  D阿基米德

• 8. 下列选项中不属于《义务教育数学课程标准》(2011年版)中统计与概率领域学习内容的是（ ）

  A掌握基本的统计概念：统计图、加权平均数、众数、中位数、平均数、方差，频数、频率、频数分布、频数分布直方图和频数折线图，抽样等

  B了解独立性检验的基本思想、方法及初步应用

  C能够根据问题的需要，有效地从事收集、整理、描述和分析数据的活动

  D能解释统计数据，根据结果做出简单的判断和预测，并进行交流

• 1. 如何处理面向全体学生与关注学生个体差异的关系

• 2. 《义务教育数学课程标准(2011年版)》中将课程标准中原来的“双基”改为了“四基”，请简述“双基”为什么要发展为“四基”。
  
  

• 3. 求绎讨点P(l．-2．0)日与盲终 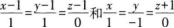都平行的平面的方程。

• 4. 设f(x)，g(x)在[a，b]上连续，在(a，b)内可导，证明：在(a，b)内存在一点ξ，使得
  

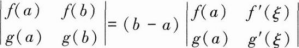
• 5. 设f(x)在[0，1]上连续，在(0，1)内可导，且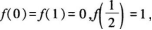试证至少存在一个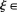  

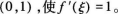
• 1. 已知函数f(x)=ex+2x2-3x。
  (1)求曲线y=f(x)在点(1,f(1))处的切线方程；
  (2)求证函数f(x)在区间[0，1]上存在唯一的极值点，并用二分法求函数取得极值时相应x
  的近似值(误差不超过0.2)；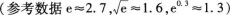 
  (3)当x≥1/2时，若关于x的不等式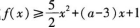 恒成立，试求实数a的取值范围。  

• 1. 阐述在数学教学过程中如何处理好教师教与学生学的关系。

• 1. 下面是某位老师引入负数概念的教学片段。
  师：我们当地7月份的平均气温是零上28℃，1月份的平均气温是零下3℃，问7月份的平均气温比1月份的平均气温高几度?如何列式计算?
  生：用零上28℃减去零下3℃，得到的答案是31℃。
  师：答案没错，算式呢?
  生：文字与数字混在一起，一点也不美观。
  生：零上28℃，我们常说成28℃，可用28表示，但是零下3℃不能说成3℃呀！也就不能用3表示。
  师：大家的发言很有道理，如何解决这一系列的矛盾呢?看样子有必要引入一个新数来表示零下3c℃。这时，零下3℃就可写成-3℃，-3就是负数。
  问题：
  (1)对该教师情境创设的合理性作出解释；
  (2)在引入数学概念时，结合上述案例，说说教师创设情境要考虑哪些因素？

• 1. 圆周角是初中九年级的上册的内容，是在圆的基本概念和性质以及圆心角概念和性质的基础上对圆周角的性质的探索，圆周角的性质在圆的有关证明、作图、计算中有着广泛的应用。
  回答下列问题：
  (1)确定圆周角一课的教学目标和教学重难点；
  (2)根据教材，设计圆周角一课引入的教学片段。要求：引导学生经历从实际背景抽象概念的过程。
  (3)分析圆周角与圆心角的不同。