初中数学学科知识与教学能力试题(二)

• 1.  

  A平行于π

  B在π上

  C垂直于π

  D与π斜交

• 2. 下列说法中正确的是（ ）

  A会重合的图形一定是轴对称图形

  B中心对称图形一定是会重合的图形

  C两个成中心对称的图形的对称点连线必过对称中心

  D两个会重合的三角形一定关于某一点成中心对称

• 3. 设a∈R，则a=1是直线l1：ax+2y-1=0与直线l2：x+(a+1)y+4=0平行的( )

  A充分不必要条件

  B必要不充分条件

  C充要条件

  D既不充分也不必要条件

• 4.  

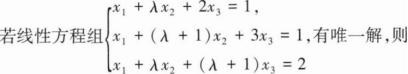
  Aλ=1

  Bλ≠1

  Cλ=2

  Dλ≠2

• 5. 设有非零向量a，b，c，若a·b=0，a×c=0，则b·c=()。

  A0

  B-1

  C1

  D3

• 6. 由曲线y=x2，y=x3围成的封闭图形的面积为()

  A1/12

  B1/4

  C1/3

  D7/72

• 7. 以下对内容标准中指数函数内容要求描述不准确的是()

  A掌握指数函数模型的实际背景

  B通过具体实例了解实数指数幂的意义，掌握幂的运算

  C在解决简单实际问题的过程中，体会指数函数是一类重要的函数模型

  D能借助计算器或计算机画出具体指数函数的图象

• 8.

• 1. 如图，用A、B、C三类不同元件连接成两个系统N1、N2，当元件A、B、C都正常工作时，系统N1正常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N2正常工作。已知元件A、B、C正常工作的概率依次为0．80、0．90、0．90。分别求系统N1、N2正常工作的概率P1、P2。
  

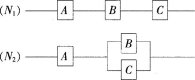
• 2. 《义务教育教学课程标准(2011年版)》对利用不等式解决实际问题的要求是：能够根据具体问题中的数量关系列出一元一次不等式，解决简单的问题。请简要分析如何进行这节课的教学。

• 3. 甲、乙、丙三车间加工同一产品，加工量分别占总量的25％，35％，40％，次品率分别为0.03，0.02，0.01。现从所有产品中取出一件，试求：
  (1)该产品是次品的概率；
  (2)若检查结果显示该产品是次品，则该产品是乙车间生产的概率是多少?

• 4.
  
  

• 5. 在数列{an}中，a1=1，an+1=2an+2n。
  (1)设, 证明：数列{bn}是等差数列；
  (2)求数列{an}的前n项和Sn。

• 1.
  (2)求γ=(9，6，5)T在这两组基下的坐标；
  (3)求向量6，使它在这两组基下有相同的坐标。

• 1. 类比思想是一种重要的数学思想，不仅可以在很多知识的理解与掌握上发挥作用，在解决很多实际问题时，这种数学思想的作用也能够很好地得到体现。请谈谈在教学过程中，类比思想对数学学习有哪些帮助?

• 1. 下面是教师讲授探索并了解：过圆外一点所画的圆的两条切线长相等的教学片段。 ①发现结论。
  在透明纸上画出如图1的图：设PA，PB是⊙O的两条切线，A，B是切点。让学生操作：沿直线OP将图形对折，启发学生思考，组织学生交流，使学生发现：PA=PB，∠APO=∠BP0。
  ②证明结论。如图2，连结OA和OB。因为以和PB是(D0的切线，所以∠PAO=∠PBO=900，即△PAD与△PBD均为直角三角形。又因为OA=OB、OP=OP，所以△POA和APOB全等。于是有PA=PB，∠APO=A_BP0。
  
  问题：
  (1)以上教学过程中，用到了哪两种推理方法；
  (2)结合案例简要阐述这两种推理方法的异同点及二者的作用；
  (3)写出你对上述教学过程的反思。

• 1. 在学习《有理数的加法》一课时，某位教师对该课进行了深入的研究，做出了合理的教学设计，根据该课内容完成下列任务：
  (1)本课的教学目标是什么
  (2)本课的教学重点和难点是什么
  (3)在情境引入的时候，某位老师通过一道实际生活中遇到的走路问题引出有理数的加法，让学生讨论得出有理数加法的两个数的符号，这样做的意义是什么