高中化学学科知识与教学能力试题(四)
考试总分:150分
考试类型:模拟试题
作答时间:120分钟
已答人数:278
试卷答案:有
试卷介绍: 高中化学学科知识与教学能力试题(四)里面有着高中化学学科知识与教学能力试题及高中化学学科知识与教学能力答案,不要走开哦。
试卷预览
-
1.
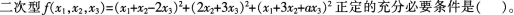
Aa<-1
Ba≠-1
Ca≠1
Da>1
-
2.
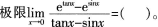
A0
B
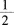
C1
D
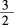
-
3.

Aƒ(x4)
Bx2 ƒ(x4)
C2xƒ(x4)
D2xƒ(x2)
-
4.
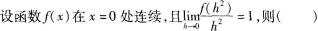
A
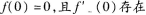
B

C

D

-
5.

A连续点
B跳跃间断点
C第二类间断点
D可去间断点
-
6.
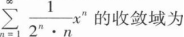
A[-2,2)
B[-2,2]
C(-2,2]
D(-2,2)
-
7. 设X是一个集合ρ=X×X→R,如果关于任何x,y,z∈X,有(i)ρ(x,y)≥0,并且ρ(x,y)=0,当且仅当x=y;(ii)ρ(x,y)=ρ(y,x);(iii)ρ(x,z)≤ρ(x,y)ρ(y,z),则称ρ是集合X的一个度量。此度量的定义方式是()。
A公理式定义
B外延式定义
C属种差异式定义
D递归式定义
-
8.
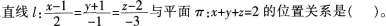
A平行
B相交但不垂直
C垂直
D直线ι在平面π上
-
9. 平面x-y+2z=8与平面2x+y+z=10的夹角是()。
A
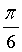
B
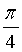
C
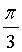
D
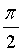
-
10. 关于二次曲面x2+y2=z2,下列说法正确的是()。
A它是一个锥面
B它是一个球面
C它是一个鞍面
D它是一个柱面
-
11. 教学方法中的发现式教学法又叫()教学法
A习惯
B态度
C学习
D问题
-
12. 设事件A,B相互独立,P(B)=0.5,P(A-B)=0.3,则P(B-A)=()。
A0.1
B0.2
C0.3
D0.4
-
13. 《学记》中提出“道而弗牵,强而弗抑,开而弗达”。这体现了下列哪项教学原则?()
A启发式原则
B因材施教原则
C循序渐进原则
D巩固性原则
-
14. 关于三角形关系的描述,初中有“大角对大边”,高中有“正弦定理”,这个研究过程的思路主要表现为()。
A从理论到实际
B从一般到特殊
C从定性到定量
D从有限到无限
-
15. “以学生发展为本”中“发展”的含义包括全体学生的发展、全面和谐的发展、终身持续的发展、个人特长的发展以及()的发展。
A科学
B可持续性
C活泼主动
D身心健康
-
16. 提出“一笔画定理”的数学家是()。
A高斯
B牛顿
C欧拉
D莱布尼兹
-
17. 对某目标进行100次独立射击,假设每次射击击中目标的概率是0.2,记X为100次独立射击击中目标的总次数,则E(X2)等于()。
A20
B200
C400
D416
-
18. 设A,B为独立的事件,且P(A)>0,P(B)>0,则下面四个式子中不成立的是( )。
AP(B|A)>0
BP(A|B)=P(A)
CP(A|B)=0
DP(AB)=P(A)·P(B)
-
19.

A

B
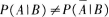
CP(AB)=P(A)P(B)
DP(AB)≠P(4)P(B)
-
20.
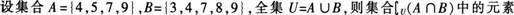 共有( )。
共有( )。A3个
B4个
C5个
D6个
-
1. 设函数f(x)在[a,b]上连续,满足f([a,b])∈[a,b]。证明:存在x0,∈[a,b],使得f(x0)=x0。
-
2.
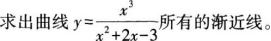
-
1. 在考试中不考建模,是不是就没必要学习建模了?结合新课程标准的相关要求,谈谈你对此观点的看法。
-
1. 案例:概念同化指从已有概念出发,理解并接纳新概念的过程,实质是利用演绎方式理解和掌握概念。由于数学中大多数概念是以属概念加种差的方式定义的,所以适宜采用概念同化的方式进行教学。
以“奇函数”概念教学为例简要说明概念同化的教学模式:
(1)向学生提供“奇函数”概念的定义
(2)解释定义中的词语、符号、式子所代表的含义
突出概念刻画的是:对定义域中的任意一个自变量x,考察x与-x对应的函数值ƒ(x)与ƒ(-x)之间的关系ƒ(-x)=-ƒ(x)。因此函数的定义域应该关于原点对称,满足这个条件后再考察ƒ(-x)=-ƒ(x)。
(3)辨别例证,深化概念
教师向学生提供丰富的概念例证,例证中以正例为主,但也要包含适当的反例,尤其是一些需要考察隐含条件的例子。
(4)概念的运用
提供各种形式来运用概念,达到强化对概念的理解,促进概念体系的建构的目的,可以利用个别有一定综合性但难度不大的问题。
问题:
(1)请举出反例说明(3)辨别例证,深化概念;
(2)请举例补充(4)概念的运用;
(3)请结合案例,总结出概念同化的教学模式的过程。
-
1. 设随机变量X在区间(0,1)服从均匀分布,求Y=eX的概率密度。
相关试卷
-
高中生物学科知识与教学能力试卷(三)275人做过
-
2017上半年教师资格证考试《高中化学》真题及答案471人做过
-
高中生物学科知识与教学能力试卷(二)444人做过
-
2018下半年教师资格证考试《高中化学》真题及答案287人做过
-
高中生物学科知识与教学能力试卷(一)164人做过
-
2018上半年教师资格证考试《高中化学》真题及答案177人做过
-
化学学科知识与教学能力高级中学模拟题(一)317人做过
-
2019上半年教师资格证考试《高中化学》真题及答案118人做过
-
高中化学学科知识与教学能力简答题(一)167人做过
-
2017下半年教师资格证考试《高中物理》真题及答案(不完整版)219人做过
相关题库