n阶方阵A可对角化的充分必要条件是
查看答案
相关试题
换一换


n阶方阵A可对角化的充分必要条件是
答案
设A是3阶方阵,A能与对角阵相似的充分必要条件是().
A.存在可逆阵P,使得P-1AP=B B.A是实对称阵 C.A有3个线性无关的特征向量 D.A有3个不同的特征值
答案
设A是3阶方阵,A能与对角阵相似的充分必要条件是( ).
A.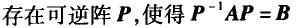 B.A是实对称阵 C.A有3个线性无关的特征向量 D.A有3个不同的特征值
B.A是实对称阵 C.A有3个线性无关的特征向量 D.A有3个不同的特征值
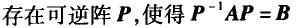 B.A是实对称阵 C.A有3个线性无关的特征向量 D.A有3个不同的特征值
B.A是实对称阵 C.A有3个线性无关的特征向量 D.A有3个不同的特征值 答案
设A是n阶方阵,则|A|=0的必要条件是( ).
A.两行(列)元素对应成比例: B.必有一行为其余行的线性组合: C.A中有一行元素全为零: D.任一行为其余行的线性组合
答案
A是n阶正定矩阵的充分必要条件是
答案
N阶实对称矩阵A正定的充分必要条件是().
A.A无负特征值 B.A是满秩矩阵 C.A的每个特征值都是单值 D.A^-1是正定矩阵
答案
设n阶矩阵A满足(aE-A)(bE-A)=O且a≠6.证明:A可对角化
答案
设n阶矩阵A满足(aE-A)(bE-A)=O且a≠6.证明:A可对角化.
答案
中国大学MOOC: n阶方阵A相似于对角矩阵的充要条件是A有n个( )。
答案
设A,B为,N阶实对称矩阵,则A与B合同的充分必要条件是().
A.r(A)=r(B) B.|A|=|B| C.A~B D.A,B与同一个实对称矩阵合同
答案
热门试题
设A为m阶正定矩阵,B为m×n阶实矩阵.证明:B^SAB正定的充分必要条件是r(B)=n,
A是n阶矩阵,且A≠0,证明:存在一个n阶非零矩阵B,使AB=0的充分必要条件是|A|=0。
设A,B都是N阶对称矩阵,证明AB是对称矩阵的充分必要条件是.AB=BA
方阵A可逆的充分必要条件是A的特征值不全为零()
方阵A可逆的充分必要条件是A的特征值不全为零
n阶行列式Dn=0的必要条件是( )。
设A为n阶矩阵,证明:r(A)=1的充分必要条件是存在n维非零列向量α,β使得A=αβT.
n阶方阵A有n个不同的特征值是A与对角阵相似的( )
n阶方阵A 有n个不同的特征值是A与对角阵相似的( )。
中国大学MOOC: n阶方阵A与某对角矩阵相似,则( ).
设A为m×n阶矩阵,则方程组AX=b有唯一解的充分必要条件是().
已知p是r的充分条件而不是必要条件,q是r的充分条件,s是r的必要条件,q是s的必要条件,现有下列命题:①s是q的充要条件;②p是q的充分条件而不是必要条件;③r是q的必要条件而不是充分条件;④﹁p是﹁s的必要条件而不是充分条件;⑤r是s的充分条件而不是必要条件。则正确命题的序号是( )。
识别的阶条件仅仅是判别模型是否可识别的必要条件而不是充分条件。( )
设A、B均为n阶方阵,A有n个互异的特征值,且AB=BA,证明:B相似于对角矩阵.
合作的充分必要条件是()
假言推理可以分为充分条件假言推理、必要条件假言推理以及充分必要条件假言推理。
节点导纳阵是n×n阶对称复数方阵
节点导纳阵是n×n阶对称复数方阵()
同余式有解的充分必要条件是()
流网存在的充分必要条件是()



 使用微信扫一扫登录
使用微信扫一扫登录