将f(x)=ln(4x-5)展开成x-2的幂级数,并指出其收敛域.
查看答案
相关试题
换一换


将f(x)=ln(4x-5)展开成x-2的幂级数,并指出其收敛域.
答案
将f(x)=1/(2-x)展开为x的幂级数,其收敛域为( )。
A.(-1,1) B.(-2,2) C.〔-1/2,1/2) D.(-∞,+∞)
答案
将f(x)=sin3x展开为x的幂级数,并指出其收敛区间。
答案
将函数f(x)=xe3x展开为x的幂级数,并指出其收敛区间.
答案
将f(x)=cos2x展开成x的幂级数.
答案
将f(x)=arctanx(|x|<1)展开成x的幂级数。
答案
函数1/x展开成(x-2)的幂级数是( )。
A.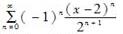 B.
B.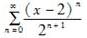 C.
C.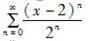 D.
D.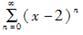
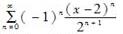 B.
B.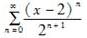 C.
C.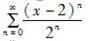 D.
D.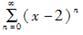
答案
函数f(x)=lnx展开成(x-2)的幂级数是()
A.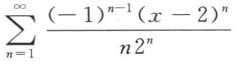 B.
B. C.
C. D.
D.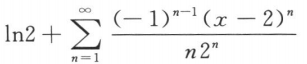
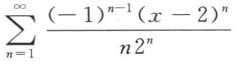 B.
B. C.
C. D.
D.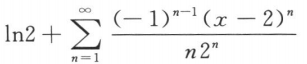
答案
将y=ex+1展开成x的幂级数。
答案
函数f(x)=ln(1-x-2x2)展开成x的幂级数为().
答案
热门试题
函数f(x)=x/(x2-5x+6)展开成(x-5)的级数的收敛区间是()
将f(x)=e-2X展开为x的幂级数.
下列结论正确的是()(1)幂级数在收敛区间内一定绝对收敛。(2)经过计算求得幂级数的收敛半径为R,则R一定是正常数。(3)幂级数在区间[-R,R]上连续。(4)幂级数的和函数S(x)在收敛域上连续。(5)幂级数在收敛域上逐项可微,可微后所得到幂级数与原级数具有相同的收敛域。(6)幂级数的收敛区间就是我们俗称的收敛域。(7)幂级数在收敛域上不可能条件收敛。(8)幂级数在收敛区间内逐项可积,可积后所得
将f(x)=e-2X展开为x的幂级数。
将f(x)=ln(1+x2)展开为x的幂级数。
试证幂级数x+x3/3!+x5/5!+…+x2n+1/(2n+1)!+…在其收敛区间内的和函数y(x)满足微分方程y′+y=ex,并求此幂级数在收敛区间内的和函数。
将下列函数展开为x的幂级数。 (1)f(x)=ln(4-3x-x2); (2)f(x)=x/(9-x2)
知幂级数的收敛半径R=1,则幂级数的收敛域为()。
幂级数的收敛域是( )。
幂级数的收敛域是( )。
将f(x)=sinx展成x-π/4的幂级数。
函数f(x)=2x在x=1处的幂级数展开式为().
将ex展开为x的幂级数,则展开式中含x3项的系数为——.
幂级数的收敛半径为2,则幂级数的收敛区间是()
将展开为关于x-1的幂级数。 解:先将f(x)写成关于x-1的函数,再利用最基本的幂级数公式展开。 。这 A=_______,B=_______/ananas/latex/p/2269790/ananas/latex/p/2269853
幂级数的收敛半径和收敛域( )/ananas/latex/p/250868
幂级数的收敛域不可能是
gx对x-1的幂级数展开式为。
幂级数在|x|
若级数[v]在x=-2处收敛,则此级数在x=5处的敛散性是怎样的?()



 使用微信扫一扫登录
使用微信扫一扫登录