在大地四边形中,观测角应该满足的角度条件可以列出我个,但其中独立的条件只有三个,通常取一个四边形内角和条件和两个对顶角条件。()
查看答案
相关试题
换一换


在大地四边形中,观测角应该满足的角度条件可以列出我个,但其中独立的条件只有三个,通常取一个四边形内角和条件和两个对顶角条件。()
答案
条件平差中,虽然大地四边形有个别角度未观测,但仍可以列出极条件方程式。
答案
四个角相等的四边形是( )。
A.A 梯形 B.B 长方形 C.C 平行四边形 D.D 正方形
答案
布设小三角网时,单三角锁、线形三角锁适用于()地带,中点多边形、大地四边形多用于()地区,大地四边形尤其适用于()中。
答案
布设小三角网时,单三角锁、线形三角锁适用于()地带,中点多边形、大地四边形多用于()地区,大地四边形尤其适用于()中
答案
四个角都相等的四边形是()
A.任意四边形 B.平行四边形 C.菱形 D.矩形
答案
下列条件中,能判定四边形ABCD为平行四边形的是()
A.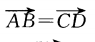 B.
B.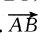
 C.
C.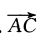
 D.
D.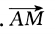
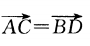
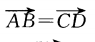 B.
B.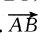
 C.
C.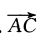
 D.
D.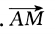
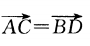
答案
设命题甲:四边形为菱形,命题乙:四边形为平行四边形,则甲是乙的必要不充分条件。()
答案
设甲:四边形ABCD是平行四边形,乙:四边形ABCD是正方形,则()。
A.甲是乙的充分条件,但不是乙的必要条件 B.甲是乙的必要条件,但不是乙的充分条件 C.甲是乙的充分必要条件 D.甲不是乙的充分条件,也不是乙的必要条件
答案
如果一个四边形是中心对称图形,那么这个四边形一定是平行四边形吗?为什么?
答案
热门试题
三角形和四边形是最基本的框架,四边形框架的稳定性最好()
三角形和四边形是最基本的框架,四边形框架的稳定性最好()
顺次连接四边形ABCD的各边中点所得的四边形是()
“四边形的四条边相等”是“四边形是正方形”的()
两角一边作图,四边形不可作
三角形∶平行四边形
三角形:平行四边形()
四边形属于()形。
已知四边形ABCD的对角线相交于O,给出下列4个条件:①AB∥CD;②AD∥BC;③AB=CD;④∠BAD=∠DCB.从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有()
已知四边形ABCD的对角线相交于o,给出下列5个条件①AB//CD②ADllBC③AB=CD④∠BAD=∠DCB,从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有()
下列说法:①一组对边相等,另一组对边平行的四边形是平行四边形;②对角线互相垂直的四边形是菱形;③有三个角是直角的四边形是矩形;④正方形的对角线相等。其中错误的有()
下列说法:①一组对边相等,另一组对边平行的四边形是平行四边形;②对角线互相垂直的四边形是菱形;③有三个角是直角的四边形是矩形;④正方形的对角线相等。其中错误的有( )
一个三角形和一个平行四边形,面积相等,底也相等,那么三角形和平行四边形的高相比较().
日常生活中,我们随处可见四边形的物体,那么有两组对边平行的四边形,这样的四边形邻角()
两个面积相等的三角形可以拼成一个平行四边形。
平行四边形四个内角度数的和()梯形四个内角度数的和。
判断一个四边形是矩形,下列条件正确的是()
小三角网的布置形式有单三角锁、中点多边形、大地四边形、线形三角形。
平面α外一点P到平面α内的四边形的四条边的距离都相等,且P在α内的射影在四边形内部,则四边形是()
“三角形”与“四边形”两个概念外延间的关系是()



 使用微信扫一扫登录
使用微信扫一扫登录