∫[(lnx-1)/x2]dx=____。
查看答案
相关试题
换一换


∫[(lnx-1)/x2]dx=____。
答案
∫[(1-lnx)/(x+alnx)2]dx=( )。
A.x/[a(x+alnx)]+C B.-x/[a(x+alnx)]+C C.(alnx)/x+C D.a(1-lnx)/x2+C
答案
设f(lnx)=x2+2lnx,则∫xf'(x)dx=()
A. B.
B.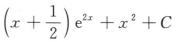 C.
C.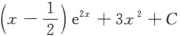 D.
D.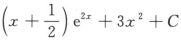
 B.
B.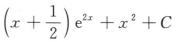 C.
C.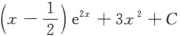 D.
D.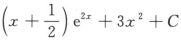
答案
∫f (x) dx=lnx+C, 则∫cosxf (cosx) dx等于()
A.cosx+C B.x+C C.sinx+C D.ln(cosx) +C
答案
∫xx(1+lnx)dx=( )。
A.xx+1/(x+1)+lnx+C B.xx+C C.xlnx+C D.xxlnx/2+C
答案
如果f(x)=e-x,则[f′(lnx)/x]dx等于:()
A.-(1/x)+c B.1/x+c C.-lnx+c D.1nx+c
答案
求函数 y=tan2(1+2x2)的微分:: -8x×tan(1+2x2)×sec2(1+2x2)dx .|8x×tan(1+2x2)×sec2(1+2x2)dx .|8x×tan(1+2x2)×sec2(1-2x2)dx .|8x×tan(1-2x2)×sec2(1+2x2)dx .
答案
若∫f(x)dx=F(x)+C,则∫xf(1-x^2)dx=( )。
A.F(1-x^2)+C B.-(1/2)F(1-x^2)+C C.(1/2)F(1-x^2)+C D.-(1/2)F(x)+C
答案
已知f´(x)=1/[x(1+2lnx)],且f(x)等于( )。
A.ln(1+2lnx)+1 B.1/2ln(1+2lnx)+1 C.1/2ln(1+2lnx)+1/2 D.2ln(1+2lnx)+1
答案
计算∫cos(lnx)dx.
答案
热门试题
∫[xex/(1+x)2]dx=____。
设∫[f(x)dx=x2+C,则∫x3f(1-x4)dx=()
函数f(x)=|2x一1 |-2lnx的最小值为_
\(\int_{0}^{+\infty }{\frac{dx}{(1+x)(1+ { { x}^{2}})}}\)=(? ? ? )。
f′(x)连续,则∫f′(2x+1)dx等于()
f′(x)连续,则∫f′(2x+1)dx等于()
设函数f(x,y)可微,且f(x+1,ex)=x(x+1)2,f(x,x2)=2x2lnx,则df(1,1)=( ).
∫ln(1+x2)dx的值为( )。
设x2+xy+y3=1,则(d2y/dx2)|x=1=____。
设f(x)满足f2(lnx)-2xf(lnx)=0,且f(x)≠0,求f(x).
证明:当x>1时,x>1+lnx.
证明:当x>1时,x>1+lnx.
设y=f[(2x-1)/(x+1)],f′(x)=ln(x^1/3),则dy/dx( )。
设∫xf(x)dx=arcsinx+C1,则∫[1/f(x)]dx=____。
已知∫f(2x-1)dx=arctanx2+C,则f(x)=()
曲线y=3x+(lnx)/(2x)+1的斜渐近线是( )。
曲线y=3x+(lnx)/(2x)+1的斜渐近线是____。
不定积分∫xcos(x2+1)dx=()
设y=f[(2x-1)/(x+1)],f′(x)=ln(x1/3),则dy/dx____。
设f′(lnx)=1+x,则f(x)=( )。



 使用微信扫一扫登录
使用微信扫一扫登录