焦点坐标为(1,0)的抛物线的标准方程是()
A. y2=-4x
B. y2=4x
C. x2=-4y
D. x2=4y
查看答案
相关试题
换一换


已知抛物线的焦点坐标是(0,-3),则抛物线的标准方程是()。
A.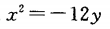 B.
B.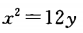 C.
C.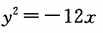 D.
D.
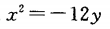 B.
B.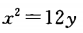 C.
C.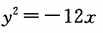 D.
D.
答案
已知抛物线的焦点坐标是(0,-3),则抛物线的标准方程为()
A.x2=-12y B.x2=12y C.y2=-12x D.y2=12x
答案
已知抛物线的焦点坐标是(0,-2),则该抛物线的标准方程是()
A.x2=-8y B.x2=8y C.y2=-8x D.y2=8x
答案
已知抛物线的焦点坐标是(-1,0),则抛物线的标准方程为()
A.x2=4y B.x2=-4y C.y2=4x D.y2=-4x
答案
已知抛物线的焦点坐标为(4,0),则此抛物线的标准方程为()
A.x2= 8y B.x2= 16y C.y2=8x D.y2=16x
答案
已知抛物线的焦点坐标为(4,0),则此抛物线的标准方程为()
A.x²=8y B.x²=16y C.y²=8x D.y²=16x
答案
焦点坐标为(1,0)的抛物线的标准方程是()
A.y2=-4x B.y2=4x C.x2=-4y D.x2=4y
答案
焦点坐标为(0,1)的抛物线的标准方程是________
答案
焦点坐标为(-2,0)的抛物线的标准方程为__________
答案
已知抛物线的标准方程y2=ax,则其焦点坐标为()
A.(a/4,0) B.(0,a/4) C.(-a/4,0) D.(0,-a/4)
答案
热门试题
已知抛物线的标准方程是y2=8x,求它的焦点坐标()
已知抛物线的标准方程为y2=4x,则其焦点坐标为()
已知抛物线的焦点在x轴上,顶点为坐标原点,且顶点到准线的距离为2/3,则抛物线的标准方程为_______.
已知抛物线的方程为标准方程,焦点在x轴上,其上一点P(—3,m)到焦点距离为5,则抛物线方程为()。
求焦点到准线的距离是2的抛物线的标准方程.
抛物线y²=-4x的焦点坐标是().
抛物线y=4x²的焦点坐标是()
已知抛物线的顶点在坐标原点,准线方程为y=4,则该抛物线的方程为()
抛物线y=5x²的焦点坐标为()
若抛物线顶点在原点,对称轴与坐标轴重合,且焦点在直钱3x一4y=12上,求这个抛物线的标准方程。
顶点在原点,焦点是(0,-2)的抛物线方程是().
抛物线的顶点在原点,对称轴为坐标轴,焦点在直线3x-4y-12=0上,求此抛物线的方程.
已知抛物线的顶点在原点,对称轴为y轴,焦点坐标F(0,1). (1)求抛物线的标准方程; (2)若过点A(0,m)且斜率为2的直线与该抛物线没有交点,求m的取值范围; (3)过焦点F且与x轴平行的直线与抛物线相交于P,Q两点,求以抛物线的焦点为圆心、PQ为直径的圆的方程.
抛物线y=ax2(a<0)的焦点坐标是()。
已知抛物线 C的焦点F在x轴的正半轴上,顶点为坐标原点,若抛物线上一点M(2,m)满足|MF|=6,则抛物线C 的方程为()
抛物线y=x2的焦点坐标为
已知抛物线的方程为y2=8x,则抛物线的焦点到准线的距离是()
抛物线y=4x2的焦点坐标是_______
抛物线y2=12x的焦点坐标是_______
抛物线4x2=y的焦点坐标是_______



 使用微信扫一扫登录
使用微信扫一扫登录