设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f′(x)≠1,证明在(0,1)内有且仅有一个x,使得f(x)=x。
查看答案
相关试题
换一换


设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f′(x)≠1,证明在(0,1)内有且仅有一个x,使得f(x)=x。
答案
设函数f(x)在闭区间[a,b]上积分>0,则f(x)在闭区间[a,b]上
答案
中国大学MOOC: 闭区间上的连续函数的值域是一个闭区间.
答案
下列说法正确的有(): 无界函数在闭区间上必定可积|狄义克雷(Dirichlet)函数在闭区间[-1,1]上可积,所以肯定能构造收敛的数值积分公式。|闭区间上有界函数只有有限个间断点,则该函数可积|闭区间上的连续函数必定可积
答案
若函数f(x)在闭区间[a,b]上连续,则f(x)在闭区间[a,b]上有界。()
A.对 B.错
答案
设函数f(x)在区间[-2,2]上可导,且f′(x)>f(x)>0,则( )。
A.f(-2)/f(-1)>1 B.f(0)/f(-1)>e C.f(1)/f(-1)<e2 D.f(2)/f(-1)<e2
答案
设函数f(x)在闭区间[a,b]上有定义,在开区间(a,b)内可导,则( )。
A.当f(a)f(b)<0时,存在ξ∈(a,b),使f(ξ)=0 B.对任何ξ∈(a,b),有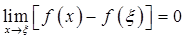 C.当f(a)=f(b)时,存在ξ∈(a,b),使f′(ξ)=0 D.存在ξ∈(a,b),使f(b)-f(a)=f′(ξ)(b-a)
C.当f(a)=f(b)时,存在ξ∈(a,b),使f′(ξ)=0 D.存在ξ∈(a,b),使f(b)-f(a)=f′(ξ)(b-a)
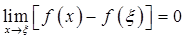 C.当f(a)=f(b)时,存在ξ∈(a,b),使f′(ξ)=0 D.存在ξ∈(a,b),使f(b)-f(a)=f′(ξ)(b-a)
C.当f(a)=f(b)时,存在ξ∈(a,b),使f′(ξ)=0 D.存在ξ∈(a,b),使f(b)-f(a)=f′(ξ)(b-a) 答案
设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则曲线y=f(x)在(a,b)内平行于x轴的切线()
A.不存在 B.只有一条 C.至少有一条 D.有两条以上
答案
设?(x)为开区间(a,b)上的可导函数,则下列命题正确的是( )
A.?(x)在(a,b)上必有最大值 B.?(x)在(a,b)上必一致连续 C.?(x)在(a,b)上必有界 D.?(x)在(a,b)上必连续
答案
在闭区间[a ,b]上连续是函数f(x)有界的( )
答案
热门试题
设f(x)为开区间(a,b)上的可导函数,则下列命题正确的是( )
设f(x)为开区间(a,b)上的可导函数,则下列命题正确的是( )。
函数f(x)在区间[a,b]上连续是它在该区间上可积的( ).
奇函数f(x)在闭区间[-1,1]上可导,且f′(x)≤M(M为正常数),则必有()《》()
对于闭区间上的连续函数,下列说法错误的是( )
设不恒为常数的函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b)。证明:在(a,b)内至少存在一点ξ,使得f′(ξ)>0。
函数f(x)在[a,b]上连续是f(x)在该区间上可积的()
函数f(x)在[a,b]上连续是f(x)在该区间上可积的()
若可导函数?(x)在区间I上单调,则其导函数?′(x)也单调。()
若可导函数?(x)在区间I上单调,则其导函数?′(x)也单调()
函数f(x)=x3在闭区间[-1,1]上的最大值为_______.
闭区间上的间断函数必无界。
函数在闭区间上一定存在最值
一个函数在某区间上导数为零,则此函数在该区间上一定为常数,反之也成立.
设函数f(x)在[a,b]上连续,满足f([a,b])https://img3.233.com/2021-05/01/161983932611411.png[a,b]。证明:存在x0∈[a,b],使得f(x0)=x0。
下列命题正确的个数是()。 (1)若f(x)是[a,b]上的连续函数,则f(x)在[a,b]上可导; (2)若函数f(x)在[a,b]上可导,则f(x)是[a,b]上的连续函数; (3)函数f(x)在[a,b]上可导是函数f(x)在[a,b]上可微的充要条件; (4)若f(x)是(a,b)上的连续函数,则f(x) 在(a,b)上可积; (5)若函数f(x)在[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
下列命题正确的个数是()。(1)若f(x)是[a,b]上的连续函数,则f(x)在[a,b]上可导;(2)若函数f(x)在[a,b]上可导,则f(x)是[a,b]上的连续函数;(3)“函数f(x)在[a,b]上可导”是“函数f(x)在[a,b]上可微”的充要条件;(4)若f(x)是(a,b)上的连续函数,则f(x)在(a,b)上可积;(5)若函数f(x)在[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
上一程序段中有了G01 指令,下一程序段如果仍然是G01,则G01可省略。
闭区间上的连续函数一定是有界的。
设函数f(x),g(x)在[a,b]上连续,且在[a,b]区间积分∫f(x)dx=∫g(x)dx,则()



 使用微信扫一扫登录
使用微信扫一扫登录