设函数f(x)在[a,b]上连续,满足f([a,b])https://img3.233.com/2021-05/01/161983932611411.png[a,b]。证明:存在x0∈[a,b],使得f(x0)=x0。
查看答案
相关试题
换一换


设函数f(t)在[0,+∞)上连续,
且满足方程,求f(t).
答案
设z=φ(x2-y2),其中φ有连续导数,则函数z满足( )。
A.x∂z/∂x+y∂z/∂y=0 B.x∂z/∂x-y∂z/∂y=0 C.y∂z/∂x+x∂z/∂y=0 D.y∂z/∂x-x∂z/∂y=0
答案
设f(x)是定义在(-∞,+∞)上的连续函数,则( ).
A.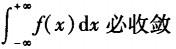 B.
B. C.
C.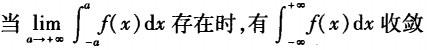 D.
D.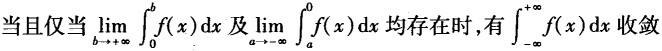
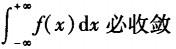 B.
B. C.
C.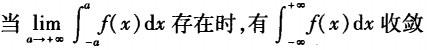 D.
D.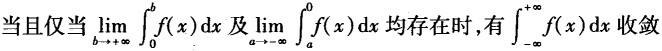
答案
设函数f(x)在[a,b]上连续且f(x)>0,则
A.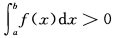 B.
B.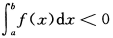 C.
C.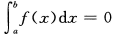 D.
D.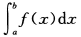 的符号无法确定
的符号无法确定
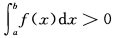 B.
B.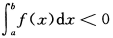 C.
C.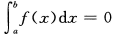 D.
D.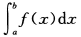 的符号无法确定
的符号无法确定 答案
设函数f(x)在[a,b]上连续且f(x)>0,则( )
A.见图A B.见图B C.见图C D.见图D E.见图E
答案
设函数f(x)在[a,b]上连续且f(x)>0,则()
A.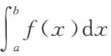 >0 B.
>0 B.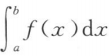 <0 C.
<0 C.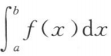 =0 D.
=0 D.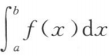 的符号无法确定
的符号无法确定
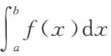 >0 B.
>0 B.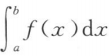 <0 C.
<0 C.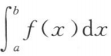 =0 D.
=0 D.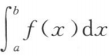 的符号无法确定
的符号无法确定 答案
设a<0,则当满足条件()时,函数f(x)=ax3+3ax2+8为增函数。
A.x0 D.x0
答案
设函数f(x)在[a,b]上连续,满足f([a,b])∈[a,b]。证明:存在x0,∈[a,b],使得f(x0)=x0。
答案
) 设?为连续函数,则(? ? ? ?).
答案
设函数,要使内连续,则=( )。
答案
热门试题
设函数f(x)在区间[a,b]上连续,则下列结论中哪个不正确()?
设函数f(x)在区间[a,b]上连续,则下列结论中哪个不正确?()
设函数f(x)在[a,b]上连续,在(a,b)可导,f"(x)>0,f(a),(b)
设函数f(x)=x2+px+q,则函数在[a,b]上满足拉格朗日中值定理结论的ξ=().
设f(x)为[a,b]上的连续函数,则下列命题不正确的是()
设函数f(x)在[a,b]上连续,在(a,b)可导,f"(x)>0,f(a)/f(b)
设函数在(a,b)内连续,则在(a,b)内()。
设函数在(a,b)内连续,则在(a,b)内()。
设?(x)为[a,b]上的连续函数,则下列命题不正确的是( )(常考)
波函数必须满足单值、有限、连续。
设函数(x)在x=0处连续,当x
若函数在上连续,则满足(1)在内连续(2)在处? ? ?连续,在处? ? ??连续。(? ?)
设f(x)是连续函数,F(x)是f(x)的原函数,则()。
设f(x)是连续的偶函数,则其原函数F(x)一定是()
设f(x)为连续函数,且下列极限都存在,则其中可推出f′(3)存在的是( )。
设f(x)在(-a,a)是连续的偶函数,且当0()
设f(x)在(-a,a)是连续的偶函数,且当0
设f(x)在(-a,a)是连续的偶函数,且当0()
设函数f(x),g(x)在[a,b]上连续,且在[a,b]区间积分∫f(x)dx=∫g(x)dx,则()
罗尔定理:设函数ƒ(x)满足条件:(1)在闭区间[a,b]上连续,(2)在开区间(a,b)内可导,(3)ƒ(a)=ƒ(b),则在(a,b)内至少存在一点ξ,使得ƒ´(ξ)=0。证明这个定理并说明其几何意义。



 使用微信扫一扫登录
使用微信扫一扫登录