证明:方程x4+4x-3=0,在(0,1)内至少有一个实根.
查看答案
相关试题
换一换


证明:方程x4+4x-3=0,在(0,1)内至少有一个实根.
答案
方程x5-3x=1在下列区间内至少有一个实根的区间是().
A.(0,1) B.(1,2) C.(2,3) D.(3,+∞)
答案
方程x-cos(x-1)=0在下列区间中至少有一个实根的区间是()
A.(-∞,0) B.(0,π) C.(π,4) D.(4,+∞)
答案
方程x-cosx-1=0在下列区间中至少有一个实根的区间是().
A.(-≥,0) B.(0,Π) C.(Π,4) D.(4,+∞)
答案
证明:方程x2ex=2至少有一个小于1的正根.
答案
若函数?(x)在[0,1]上连续,在(0,1)可导。 (1)若?(1)= ?(0)+3,证明:存在ξ∈(0,1),使得?′(ξ)=3。(5 分) (2)若?(1)=0,求证方程 x?′(x)+?(x)=0 在(0,1)内至少有一个实根。(5 分)
答案
设函数?(x)在 R 上连续且可导。 (1)当?(x)=x2,且 g(x)=ex?(x)时,求证?(x)与 g(x)有共同驻点。(4 分) (2)当?(a)=f(b)=0(a<b)时,求证方程?′(x)+ ?(x)=0 在(a,b)内至少有一个实根。(6 分)
答案
下列区间中,使方程x4+x-1=0至少有一个根的区间是()
A.(1,2) B.(2,3) C.(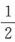 ,1)) D.(0,
,1)) D.(0,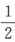 )
)
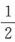 ,1)) D.(0,
,1)) D.(0,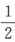 )
) 答案
已知函数f(x)在闭区间[a,b].上连续,且f(a).f(b)<0,请用二分法证明f(x)在(a,b)内至少有一个零点。
答案
已知函数 f(x)在闭区间[a,b].上连续,且 f(a).f(b)<0,请用二分法证明 f(x)在(a,b)内至少有一个零点
答案
热门试题
证明方程至少有一个小于1的正根。/ananas/latex/p/318528
证明:方程x3-3x+1=0有且仅有三个实根.
皇太极袭扰关内至少有:()
证明:方程5x+arctanx+4sinx-1=0在区间(0x1)内有唯一实根.
至少有一个证据是可信的 至少有一个证据是不可信的
设二元函数f(x,y)有连续偏导数,并且f(1,0)=f(0,1)。证明:在单位圆周上至少有两点满足方程y·∂f(x,y)/∂x=x·∂f(x,y)/∂y。
设函数f(x)在[a,b]上连续,则f(a) f(b)<0是方程f(x)=0在(a,b)上至少有一根的( )。
证明方程x5+x-1=0只有一个正根。
设f(x)=(x-1)(x-2)…(x-2019),则方程f′(x)=0有()个实根。
设函数f(x),g(x)在[a,b]上连续,在(a,b)内可导,且对于(a,b)内一切x有f′(x)g(x)-f(x)g′(x)≠0.证明:如果f(x)在(a,b)内有两个零点,则介于两个零点之间,g(x)至少有一个零点.
在机坪上每个站位或者沿机坪长度每隔()内至少有一个灭火器材箱。
每一个矿井必须至少有()井筒。
每个顺序功能图至少有一个()
每个进程至少有一个执行线程
方程x2-2x+3=0没有实根。()
设f (x) =x (x-1) (x-2),则方程=0的实根个数是()
每一个矿井必须至少有3个井筒。
每一个矿井必须至少有3个井筒。
设f (x) =x (x-1) (x-2),则方程f (x) =0的实根个数是( )。
已知x1,x2是方程x2-ax-1=0的两个实根,则x12x22=



 使用微信扫一扫登录
使用微信扫一扫登录