证明:方程5x+arctanx+4sinx-1=0在区间(0x1)内有唯一实根.
查看答案
相关试题
换一换


证明:方程5x+arctanx+4sinx-1=0在区间(0x1)内有唯一实根.
答案
曲线y=(x+4sinx)/(5x-2cosx)的水平渐近线方程为____。
答案
在区间(-∞,+∞)内方程|x|1/4+|x|1/2-cosx=0( )。
A.无实根 B.有且仅有一个实根 C.至少有两个实根 D.有无穷多个实根
答案
曲线y=sinx在点x=0处的法线方程为()
A.x+2y+=0 B.x-y=0 C.x-2y=0 D.x+y=0
答案
设随机变量ζ在区间[0,5]上服从均匀分布,则方程4x2+4ζx+2=0有实根的概率为()。
A. B. C. D.
答案
证明方程x5+x-1=0只有一个正根。
答案
证明:方程x4+4x-3=0,在(0,1)内至少有一个实根.
答案
方程x-lnx-2=0在区间(0,+∞)内( )。
A.没有实根 B.只有一个实根 C.有两个相异的实根 D.有两个以上相异实根
答案
下列区间中,使方程x4+x-1=0至少有一个根的区间是()
A.(1,2) B.(2,3) C.(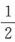 ,1)) D.(0,
,1)) D.(0,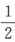 )
)
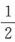 ,1)) D.(0,
,1)) D.(0,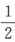 )
) 答案
设函数f(x)=x3+5sinx,则f’(0)=()()。
A.5 B.0 C.3 D.1
答案
热门试题
设函数y=y(x)由方程x2+y3-sinx+3y=0所确定,求函数y=y(x)在x=0处的法线方程。
设函数y=y(x)由方程ln(x2+y)=x3y+sinx确定,则(dy/dx)|x=0=____。
设函数y=y(x)由方程ln(x^2+y)=x^3y+sinx确定,则(dy/dx)|x=0=( )。
微分方程y^(4)-y=e^x+3sinx的特解可设为( )。
以下程序段中循环语句()x%=0DoWhilex=0x=x+1printxLoop
已知方程x4-6x2-9x=0有一正根x=3,证明:方程4x3-12x-9=0必有一个小于3的正根.
解方程:x²+4x+3=0()
求方程f(x)=0在区间[0,1]内的根,要求误差不超过10-4,那么二分次数n十1≥( )。
过点P(5,0)与圆x2+y2-4x-5=0相切的直线方程是( )
设函数ψ(x)具有二阶连续导数,且ψ(0)=ψ′(0)=0,并已知yψ(x)dx+[sinx-ψ′(x)]dy=0是一个全微分方程,则ψ(x)等于( )。
和直线3x-4y+5=0关于x轴对称的直线方程是
方程x^2-5x+4=0的两根的等比中项是()
曲线y=xarctanx的凹区间为()
设函数φ(x)具有二阶连续导数且φ(0)=0,并且已知yφ(x)dx+[sinx-φ(x)]dy=0是一个全微分方程,则φ(x)=( )。
材料全屏证明方程在区间(0,2)内必有根。14【实务操作】设则在上连续,当x=0时,当x=2时,,即。根据零点定理:,即在区间(0,2)内必有根。
若f(x)在区间[a,+∞)上二阶可导,且f(a)=A>0,f′(a)<0,f″(x)<0(x>a),则方程f(x)=0在(a,+∞)内( )。
已知函数f(x)=sinx,x<和=0 ,x不等于0,x>0,则f(0)=().
在区间0≤x≤π上研究方程sin3xcosx=a(a>0)的实根的个数。
当x→0时,x-sinx是x的().
下列区间为函数f(x)=sinx的单调增区间的是().



 使用微信扫一扫登录
使用微信扫一扫登录