已知∆ABC内,AB=2,BC=4,∠ABC=45°,BC在a内,且∆ABC所在平面与平面a成30°,则∆ABC在a内射影的面积是()
A. 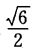 B.
B. 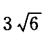 C.
C. 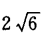 D.
D. 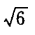
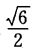
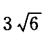
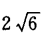
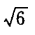
查看答案
相关试题
换一换


已知∆ABC内,AB=2,BC=4,∠ABC=45°,BC在a内,且∆ABC所在平面与平面a成30°,则∆ABC在a内射影的面积是()
A.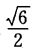 B.
B.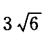 C.
C.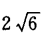 D.
D.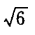
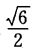 B.
B.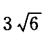 C.
C.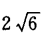 D.
D.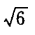
答案
已知△ABC中,A=60°,AB=AC=2,求:(1)BC;(2)△ABC的面积。
答案
已知△ABC中,A=30°,AC=BC=1求(1)AB;(2)△ABC的面积.
答案
在∆ABC中,∠ABC=600,AB=4,BC=6,则AC=()。
A.128 B.76 C.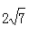 D.
D.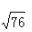
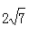 D.
D.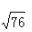
答案
在△ABC中,AB=4,BC=6,∠ABC=60°,则AC=()。
A.128 B.76 C.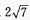 D.
D.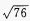
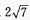 D.
D.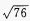
答案
已知△ABC中,A=30°,AC=BC=1.求(Ⅰ)AB;(Ⅱ)△ABC的面积.
答案
在△ABC中,若AB=3,A=45°,C=30°,则BC=()。
A.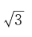 B.
B.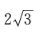 C.
C.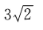 D.
D.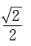
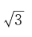 B.
B.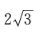 C.
C.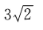 D.
D.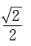
答案
在△ABC中,若AB=3,A=45°,C=30°,则BC=()。
A.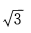 B.
B. C.
C. D.
D.
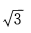 B.
B. C.
C. D.
D.
答案
在△ABC中,若B=30°,BC=4,AB=5,则△ABC的面积为()
答案
已知△ABC中,A=30°,AC=BC=1.求(I)AB;(II)△ABC的面积
答案
热门试题
在△ABC中,已知AB=3,BC=5,AC=7,则cosB=______。
在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积。
在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积
表达式max('A','ab','AB','abc','bc')的值是()。
已知△ABC中,A=110°,AB=5,AC=6,求BC.(精确到0.01)
已知△ABC中,A=110°,AB=5,AC=6,求BC.(精确到0.01)
设A(1,2,3),B(-1,2,0),C(1,1,1)则AB(→)·BC(→)=____,AB(→)×BC(→)=____,△ABC的面积=____。
已知△ABC的三边长AC=3,BC=4,AB=5,P为AB边上任意一点,则CP→ (BA→-BC→)的最大值为( )
已知△ABC的三边长AC=3,BC=4,AB=5,P为AB边上任意一点,则CP→ (BA→-BC→)的最大值为()
在Rt△ABC中,∠C为直角,BC=1/2AB,则∠A()
在△ABC中,AB=3,BC=5,AC=7,则cosB=()。
在三角形 ABC 中, AB=4 , AC=6 ,BC=8 ,D 为 BC 中点,则 AD= ()
设正整数a,b,c,满足a
设a、b、c皆为质数,且a+b+c=94,ab+bc+ac=2075,abc的值为:
函数F=AB+BC,使F=1的输入ABC组合为( )
函数F=AB+BC,使F=1的输入ABC组合为()
函数F=AB+BC,使F=1的输入ABC组合为()
函数F =AB+BC,使F=1的输入ABC组合为()
已知直线AB的方位角aAB= 87°,β右= 290°,则直线BC的方位角aBC为()
在△ABC中,∠B=60°,AB=2,M是BC的中点,AM =2√3,则AC=_______,cos∠MAC=_______



 使用微信扫一扫登录
使用微信扫一扫登录