设函数,f(x)在[a,b]上连续,且F/(x)=f(x),有一点x0∈(a,b)使,f(x0)=0,且当a≤x≤x0时,f(x)>0;当x0<x≤b时,f(x)<0,则f(x)与x=a,x=b,x轴围成的平面图形的面积为()。
A. 2F(x0)-F(b)-F(a)
B. F(b)-F(a)
C. -F(b)-F(a)
D. F(a)-F(b)
查看答案
相关试题
换一换


设函数f(x)在[a,b]上连续且f(x)>0,则
A.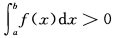 B.
B.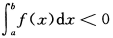 C.
C.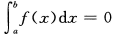 D.
D.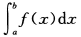 的符号无法确定
的符号无法确定
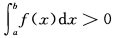 B.
B.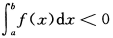 C.
C.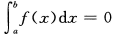 D.
D.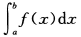 的符号无法确定
的符号无法确定 答案
设函数f(x)在[a,b]上连续且f(x)>0,则( )
A.见图A B.见图B C.见图C D.见图D E.见图E
答案
设函数f(x)在[a,b]上连续且f(x)>0,则()
A.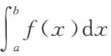 >0 B.
>0 B.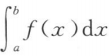 <0 C.
<0 C.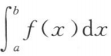 =0 D.
=0 D.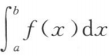 的符号无法确定
的符号无法确定
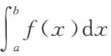 >0 B.
>0 B.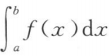 <0 C.
<0 C.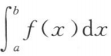 =0 D.
=0 D.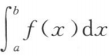 的符号无法确定
的符号无法确定 答案
设y=f(x)在[a,b]上连续,在(a,b)内可导,若存在唯一点x0∈(ab),使f′(x0)=0,且在x0左右两侧f′(x)异号,则点x=x0必为f(x)的()
A.极值点且为最值点 B.极值点但不是最值点 C.最值点但非极值点 D.以上都不对
答案
设函数,f(x)在[a,b]上连续,且F/(x)=f(x),有一点x0∈(a,b)使,f(x0)=0,且当a≤x≤x0时,f(x)>0;当x0<x≤b时,f(x)<0,则f(x)与x=a,x=b,x轴围成的平面图形的面积为()。
A.2F(x0)-F(b)-F(a) B.F(b)-F(a) C.-F(b)-F(a) D.F(a)-F(b)
答案
设函数f(x)和g(x)均在区间[a,b]上连续,在区间(a,b)内可导,且f(a)=f(b)=0,证明:存在一点ξ∈(a,b),使得f’(ξ)+2f(ξ)g(ξ)g’(ξ)=0。
答案
设函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,k为正整数,求证:存在一点ξ∈(0,1),使得ξf′(ξ)+kf(ξ)=f′(ξ).
答案
设函数f(x)在[a,b]上二阶可导f(a)=f(b)=0,且存在一点c∈(a,b)使得f(c)0。证明:至少存在一点ξ∈(a,b),使得f''(ξ)0。
答案
设函数f(x)在区间[0,2]上连续,在区间(0,2)内可导,且f(0)=f(2)=f(1)=2,证明:至少存在一点ξ∈(0,2),使得f′(ξ)=ξ.
答案
设在[0,+∞]上函数f(x)有连续导数,且f′(x)≥k>0,f(0)<0,证明:在(0,+∞]内有且仅有一个零点。
答案
热门试题
设在[0,+∞]上函数f(x)有连续导数,且f′(x)≥k>0,f(0)
设函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),证明:若f(x)不恒为常数,则至少存在一点ξ∈(a,b),使得f′(ξ)>0.
设函数f(x)连续,且f′(0)>0,则存在δ>0,使得( )。
设f(x)在[0,2]上连续,在(0,2)内可导,且f(0)+f(1)=4,f(2)=2,试证明必存在一点ξ∈(0,2),使f′(ξ)=0.
设函数f(x)在(0,1)上可导且在[0,1]上连续,且f'(x)>0,f(0)<0,f(1)>0,则f(x)在(0,1)内()。
设f(x)在内连续,且f(x)>0,证明函数在(0,+∞)内为单调增函数。
设函数f(x)在闭区间[0,4]上连续,且有f(0)=f(4)≠f(2),证明:在区间(0,2)内至少存在一点ξ,使得f(ξ)=f(2+ξ).
若f(x)有三阶导数,且f(0)=f(1)=0,设F(x)=x3f(x),试证明在(0,1)内至少存在一点ξ,使F′′′(ξ)=0.
设函数f(x)在点x=O的某邻域内具有连续的二阶导数,且f′(0)=f″(0)=0,则( )。
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0,f"(x)>0,则在(-∞,0)内必有()。
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f(x)>0,f(x)>0,则在(-∞,0)内必有( )。
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f"(x)>0, f""(x)>0,则在(-∞,0)内必有:
设f(x)是(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论()
设f(x)在(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论( )。
设不恒为常数的函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b)。证明:在(a,b)内至少存在一点ξ,使得f′(ξ)>0。
设f(x),f′(x)在[a,b]上连续,f″(x)在(a,b)内存在,f(a)=f(b)=0,且存在c∈(a,b)使f(c)>0。证明:必∃ξ∈(a,b)使f″(ξ)<0。
设f(x)在(-a,a)是连续的偶函数,且当0()
设f(x)在(-a,a)是连续的偶函数,且当0()
设f(x)在(-a,a)是连续的偶函数,且当0
设偶函数f(x)具有二阶连续导数,且f″(0)≠0,则x=0( )。



 使用微信扫一扫登录
使用微信扫一扫登录