相关试题
换一换


符号函数可以看作是双边指数衰减函数当a → 0时的极限形式。()
A.正确 B.错误
答案
在下列函数中,当x→0时,函数f(x)的极限存在的是().
A.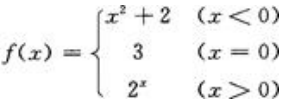 B.
B.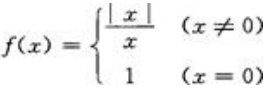 C.
C.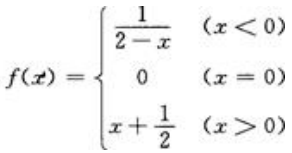 D.
D.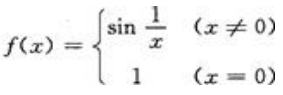
 B.
B.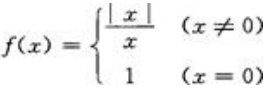 C.
C.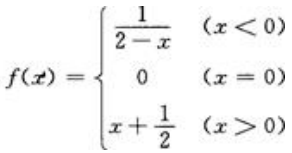 D.
D.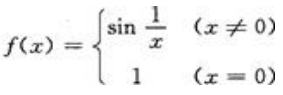
答案
函数???当???时有极限,极限为0。
答案
当x→0时,下列函数以零为极限的是()。
A.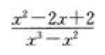 B.
B.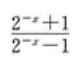 C.
C.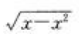 D.
D.
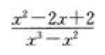 B.
B.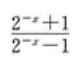 C.
C.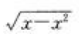 D.
D.
答案
如果函数f(x)当x→x0时极限存在,则函数f(x)在点x0处( )。
A.有定义 B.无定义 C.不一定有定义 D.连续
答案
消费函数可以看作是( )之间的函数关系。
A.消费与收入 B.储蓄与收入 C.消费与储蓄 D.消费与投资
答案
当自变量无限接近于1时,函数无限接近于-1,下列说法正确的是:: 函数的极限是 -1|函数的极限是-1(x->1)|函数的极限是1|函数的极限是1(x->1)
答案
定义函数时,形参的类型说明可以放在函数体内。
答案
当x→0时,函数sinx+cosx-1是函数x3的()
A.高阶无穷小 B.低阶无穷小 C.同阶但非等价无穷小 D.等价无穷小
答案
当消费函数为c=a+by时,a>0,0()
A.大于边际消费倾向 B.小于边际消费倾向 C.等于边际消费倾向 D.以上三种情况都有可能
答案
热门试题
当t=0时,自相关函数值Rx(0)=()。
若ƒ(x)在0某邻域(0除外)内均有ƒ(x)≥0(或ƒ(x)≤0),且函数ƒ(x)当x趋于0时极限为A,那么A≥0(或A≤()
以下描述正确的是()。: 调用函数时,实参与形参可以共用内存单元 调用函数时,实参与形参的类型必须一致 调用函数时,实参可以是表达式 调用函数时,将为形参分配内存单元
求函数在x=0点的右极限。
如果函数没有形参,则函数定义时形参列表可以省略,即函数定义"int fun {...}"是正确的。()
下列函数中,当x>0时,函数值y随x的增大而减小的是()
在定义函数重载时,函数名相同的函数形参列表也可以完全一样。()
当功能函数Z≤0时,结构处于()状态。
当功能函数Z≤0时,结构处于()状态
幂函数的原函数一定是: 对数函数|幂函数|指数函数|指数函数或对数函数
下列关于激活函数的说法中,错误的是__。A.如果激活函数的输出不是以0为均值的,可能会影响收敛速度B.使用logistic函数作为激活函数时,神经网络的输出可以看作概率C.使用Tanh函数来代替logistic函数,可以避免梯度消失问题D.sigmoid函数存在梯度消失问题()
当x→0时,下列函数是无穷大量的是()。
当x→0时,以下函数是无穷小量的是()。
设?(x)在0某邻域(0除外)内均有?(x)≥0(或?(x)≤0),且函数?(x)当x趋于0时以A为极限,则A≥0(或A≤0)。(1.0分)
设y=y(x)是二阶常系数微分方程满足初始条件y(0)=y′(0)=0的特解,则当x→0时,函数的极限()
下列函数是指数函数的是( )。
填空: 对于函数y=3/x,当x>0时,y___0,这部分图像在第_____象限;对于函数y=-3/x当x
若函数y=(a2-3a+3)ax(a>0且a≠1)是指数函数,则α=().
设函数y=f(x)的导函数,满足f′(一1)=0,当x<-l时,f′(x)<0;当x>-l时,f′(x)>0.则下列结论肯定正确的是( ).《》( )
当输入量是阶段跃函数时,输出量只按指数函数逐渐变化的环节,称为()环节。



 使用微信扫一扫登录
使用微信扫一扫登录