如果把圆柱的侧面沿高展开后得到一个正方形,那么圆柱的高等于()
A. 底面直径
B. 底面直径的л倍
C. 底面半径的л倍
查看答案
相关试题
换一换


如果把圆柱的侧面沿高展开后得到一个正方形,那么圆柱的高等于()
A.底面直径 B.底面直径的л倍 C.底面半径的л倍
答案
一个圆柱的侧面展开图是正方形这个圆柱的高和底面半径的比值是()
A.兀 B.2兀 C.3兀 D.2
答案
一个圆柱的侧面展开图是一个正方形,这个圆柱的底面半径与高的比是()
A.1:2π B.1:4π C.1:π
答案
一个圆柱的侧面展开图是正方形,那么它的侧面积是下底面积的( )倍
A.2 B.4 C.4π D.π E.2π
答案
一个圆柱的侧面展开图是一个正方形,这个圆柱的表面积与侧面积的比是().
A. B.
B. C.
C.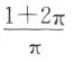 D.
D.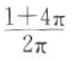
 B.
B. C.
C.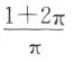 D.
D.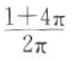
答案
底面周长和高相等的圆柱,侧面沿高展开后得到一个()
A.正方形 B.长方形 C.平行四边形
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是()。
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是()
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是( ).
A.4πS B.( l+4π)S C.(2+4π)S D.(3+4π)S
答案
一圆柱底面积为S,侧面展开图为正方形,则这个圆柱的全面积为( )
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
热门试题
圆柱底面周长和高相等时,沿着它的一条高剪开,侧面是一个正方形()
圆柱的侧面展开得到一个长方形,它的长相当于圆柱的()
圆柱的侧面展开得到一个长方形,它的宽相当于圆柱的()
一个圆柱的侧面展开图是一个边长为62.8厘米的正方形,这个圆柱的侧面积是()平方厘米,它的表面积是()平方厘米
把一个正方形的一边减少20%,另一边增加2米。得到一个长方形,它与原正方形的面积相等,那么,正方形面积是多少平方米?( )
:我们知道,一个正方形可以剪成4个小正方形,那么一个正方形能否剪成9个正方形,能否剪成11个正方形(大小不一定要相同)( )
我们知道,一个正方形可以剪成4个小正方形,那么一个正方形能否剪成11个正方形,能否剪成13个正方形(大小不一定相同):
把一个正方形按1∶3的比缩小后,正方形缩小前后的面积比是()
已知圆柱的轴截面是面积为4的正方形,则圆柱体的体积是()
把边长是a的正方形铁皮的四角切去相等的正方形,再将它折起,做成一个无盖且底面为正方形,高为切去的正方形边长的箱子,箱底边多长时,箱子的容积最大?
要拼成一个大正方形至少需要()个小正方形
一个正方形能分成 4 个正方形 能分成 11 个正方形吗 大小不一定相等?
如图中的正方形、圆柱和圆锥底面积相等,高也相等,下面哪句话是正确的?( )
已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是()
已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是( )
(2018·徐州)下列平面展开图是由5个大小相同的正方形组成,其中沿正方形的边不能折成无盖小方盒的是()
如图,将正方形边长三等分后可得9个边长相等的小正方形,把中间的小正方形去掉,对剩下的8个小正方形,均按上面方法操作。问:对一个边长为2的正方形如此操作三次后所剩白色区域的面积是多少?
搭一个正方形需要4根小棒,搭a个正方形需要()根小棒。
用两个同样大小的正方形可以拼成一个大的正方形()
如果有一个正方形被任意的两条线段分成了4个长方形,这4个长方形周长的和是200米,那么,原来正方形的边长是多少米?()



 使用微信扫一扫登录
使用微信扫一扫登录