当x趋于0时,(tan(6x)-cos(x)+1)/sin(3x)=()。
查看答案
相关试题
换一换


当x趋于0时,(tan(6x)-cos(x)+1)/sin(3x)=()。
答案
设f′(sin2x)=cos2x+tan2x,当0<x<1时,求f(x)。
答案
在区间0≤x≤π上研究方程sin3xcosx=a(a>0)的实根的个数。
答案
设tan α,tan β是方程x2+6x+7=0的两根,求证:sin(α+β)=cos(α+β).
答案
对于函数y=sin(tanx)-tan(sinx)(0≤x≤π),x=π/2是( )。
A.连续点 B.第一类间断点 C.可去间断点 D.第二类间断点
答案
当x趋于0时,若sin2x与xk是等价无穷小量,则k=().
A.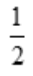 B.1 C.2 D.3
B.1 C.2 D.3
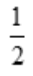 B.1 C.2 D.3
B.1 C.2 D.3 答案
当x→0时,f(x)=tan2x/x的极限是()。
A.0 B.1 C.2 D.1/2
答案
当x→0时,α(x)=sin2x和β(x)=x3+3x都是无穷小,则α(x)是β(x)的().
A.高阶无穷小 B.低阶无穷小 C.同阶且非等价的无穷小 D.等价无穷小
答案
当x→0时,5x-sin5x是x的()。
A.高阶无穷小量 B.等价无穷小量 C.同阶无穷小量,但不是等价无穷小量 D.低阶无穷小量
答案
函数f(x)=cos3xcosx-sin3xsinx的最小正周期为().
A. B.
B.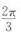 C.π D.2π
C.π D.2π
 B.
B.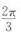 C.π D.2π
C.π D.2π 答案
热门试题
设F(x)是f(x)的原函数,当x≥0时有f(x)F(x)=sin22x,且F(0)=1,F(x)≥0,求f(x)。
已知当x→0时,函数f(x)=3sinx-sin3x与cxk是等价无穷小,则( )。
当x→0时,3x-1是x的:
若ƒ(x)在0某邻域(0除外)内均有ƒ(x)≥0(或ƒ(x)≤0),且函数ƒ(x)当x趋于0时极限为A,那么A≥0(或A≤()
(2011)当x→0时,3x-1是x的:()
当x→0时,若x-tan x与x^k是同阶无穷小,则k=
绘出以下函数的曲线:y=5*sin(x)+cos(3*x)y=sin(x)+sin(6*x)/10
设?(x)在0某邻域(0除外)内均有?(x)≥0(或?(x)≤0),且函数?(x)当x趋于0时以A为极限,则A≥0(或A≤0)。(1.0分)
已知tan x=-2,x为第四象限角,则sin x=().
方程组 x+y+z=0, ? ? ? ? (1) x+(sin2)y+(sin3)z=0 (2) 的图象是:
Raptor中SIN(X)、COS(X)和TAN(X)函数的参数X的单位是( )。
设函数(x)=1+sin2x,求"(0).
设函数ƒ(x)=1+sin2x,求ƒ'(0)。
已知z=3sin(sin(xy)),则x=0,y=0时的全微分dz()
已知f′(2+cosx)=sin2x+tan2x,则f(x)=____。
当x趋于无穷大时,1-cos(x)~0.5x2。()
已知tanα,tanβ是方程2x2-4x+1=0的两根,则tan(α+β)=()。
已知tanα,tanβ是方程2x2-4x+1=0的两根,则tan(α+β)=()。
设函数$f(x)={((sin2x)/(x),x<0),(3x^2-2x+k,x≥0):}$在$x=0$点连续,则$k=$()
f(x)=x2ln(1-x),当n≥3时,f(n)(0)=( )。



 使用微信扫一扫登录
使用微信扫一扫登录