设总体X服从于泊松分布P(λ),(X1,X2,…,Xn)是来自总体X的一个样本。
(1)写出(X1,X2,…,Xn)的概率分布;
(2)计算E(X(_)),D(X(_)),E(S2);
(3)设总体的容量为n=10的一组样本的观察值为(4,3,3,4,2,1,6,5,4,8),试求样本均值,样本方差和经验分布函数。
查看答案
相关试题
换一换


设总体X服从参数为λ的泊松分布,其中λ未知.X1,…,Xn是取自总体X的样本,则λ的最大似然估计是( ).
A.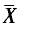 B.
B.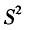 C.S D.
C.S D.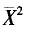
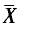 B.
B.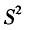 C.S D.
C.S D.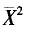
答案
设总体X服从于泊松分布P(λ),(X1,X2,…,Xn)是来自总体X的一个样本。 (1)写出(X1,X2,…,Xn)的概率分布; (2)计算E(X(_)),D(X(_)),E(S2); (3)设总体的容量为n=10的一组样本的观察值为(4,3,3,4,2,1,6,5,4,8),试求样本均值,样本方差和经验分布函数。
答案
设离散型随机变量X服从于参数为λ(λ>0)的泊松分布,已知P{X=1}=P{X=2},则λ=____。
答案
设总体X服从参数为λ的泊松分布,其中λ未知.X1,…,X是取自总体X的样本,则A的最大似然估计是().
A.X B.S2 C.S D.2
答案
设X1,X2,…,Xn是来自总体X的样本,则是( )
答案
设X服从λ=2的泊松分布,则P(X≤1)约为( )。
A.135 B.406 C.271 D.以上都不对
答案
设随机变量是Xi服从于参数λi(i=1,2)的泊松分布,且X1、X2相互独立,则P{X1=i|X1+X2=k}=____.
答案
设总体X~U(θ,θ),X1,X2,…,Xn是来自总体X的样本,求θ1,θ2的矩估计和最大似然估计.
答案
设X服从泊松分布,已知2P(X=1)=P(X=2),求P(X=3)及D(X).
答案
设随机变量X、Y相互独立,且分别服从于参数为λ1和λ2的泊松分布,则X、Y的联合分布律为P{X=m,Y=n}=____.
答案
热门试题
设随机变量X服从泊松分布,且P{X=1}=P{X=2},则E(X)=()
设总体X服从于分布f(x,λ)=e-|x|/λ/(2λ)(-∞<x<+∞)其中λ>0。若取得样本值X1,X2,…,Xn,试求: (1)E(|X|),E(|X2|); (2)参数λ的极大似然估计值λ(∧); (3)λ(∧)是否为参数A的无偏估计量?
设总体X~N(μ0,σ2),μ0为已知常数,(X1,X2,…,Xn)为来自正态总体X的样本,则检验假设H0:σ2=σ02;H1:σ2≠σ02的统计量是____;当H0成立时,服从____分布。
设随机变量X服从参数为1的泊松分布,则P{X=E(X2)}=____。
设随机变量X服从参数为1的泊松分布,则P{X=E(X2)}=( )。
设随机变量X1,X2,…,Xn相互独立,且均在区间[0,θ]上服从于均匀分布,设Y1=max{X1,X2,…,Xn},Y2=min{X1,X2,…,Xn},求E(Y1),E(Y2),D(Y1),D(Y2)。
设随机变量X1,X2,…,Xn相互独立,且均在区间[0,θ]上服从于均匀分布,设Y1=max{X1,X2,…Xn},Y2=min{X1,X2,…Xn},求E(Y1),E(Y2),D(Y1),D(Y2).
设X1,X2,…,Xn是来自正态总体N(μ,σ2)的一个样本,则有( )。
设总体X的数学期望为μ, X1,X2,…,Xn为来自X的样本,则X1是μ的无偏估计
设随机变量X服从参数为λ的泊松分布,且已知E[(X-1)(X-2)]=1,则λ=____。
设随机变量x服从参数为λ的泊松分布,且P(x=1)=P(x=2),则P(x>2)的值为()
设X1,X2,…,Xn相互独立且同服从分布B(1,p),Z=X1+X2+…+Xn,证明Z~B(n,p)。
设X,Y是相互独立且同服从于参数为λ的泊松分布的随机变量,即P{X=k}=λke-λ/k!,其中λ>0,k=0,1,2,…。求: (1)M=max(X,Y)的分布率; (2)N=min(X,Y)的分布率。
设随机变量X服从正态分布N(1,2),Y服从泊松分布P(2)。求期望E=(2X—y+3)。
设随机变量X在[-π,π]上服从于均匀分布,求:(1)E[min(|X|,1)]; (2)E[max(|X|,1)].
设总体X~N(μ,σ^2),X1,X2,…,xn为总体的简单样本,S^2为样本方差,则D(S^2)=_______.
设总体X服从【-a,a】上的均匀分布(a>0),X
设总体X~N(20,169),已知1x,2x,…,100x是来自X的样本。则样本均值的分布服从均值为20、方差为16.9的正态分布。
设总体X的分布率为P{X=x}=(1-p)x-1p,x=1,2,…;X1,X2,…,Xn是来自X的样本,试求(1)p的矩估计量;(2)p的极大似然估计量。
设总体X的分布率为P{X=x}=(1-p)x-1p,x=1,2,…;X1,X2,…,Xn是来自X的样本,试求: (1)p的矩估计量; (2)p的极大似然估计量。



 使用微信扫一扫登录
使用微信扫一扫登录