已知级数的收敛域为[-1,3),则级数的收敛域为().
A. [-2,2)
B. [-1,2)
C. (-1,2]
D. (-2,2]
查看答案
相关试题
换一换


已知级数的收敛域为[-1,3),则级数的收敛域为().
A.[-2,2) B.[-1,2) C.(-1,2] D.(-2,2]
答案
知幂级数的收敛半径R=1,则幂级数的收敛域为()。
A.(-1,l] B.[-1,1] C.[-1,1) D.(-∞,+∞)
答案
级数的收敛域是( )。
A.(一1,1) B.[-1,1] C.[-1, 0) D.(-1, 0)
答案
级数的收敛域是()。
A.(-1,1) B.[-1, 1] C.[-1,0) D.(-1,0)
答案
幂级数的收敛域是( )。
A.[-1,1] B.(-1,1] C.[-1,1) D.(-1,1)
答案
幂级数的收敛域是( )。
A.[-2,4) B.(-2,4) C.(-1,1) D.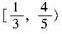
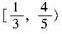
答案
下列结论正确的是()(1)幂级数在收敛区间内一定绝对收敛。(2)经过计算求得幂级数的收敛半径为R,则R一定是正常数。(3)幂级数在区间[-R,R]上连续。(4)幂级数的和函数S(x)在收敛域上连续。(5)幂级数在收敛域上逐项可微,可微后所得到幂级数与原级数具有相同的收敛域。(6)幂级数的收敛区间就是我们俗称的收敛域。(7)幂级数在收敛域上不可能条件收敛。(8)幂级数在收敛区间内逐项可积,可积后所得
A.(1)(8) B.(1)(7) C.(1)(3)(8) D.(1)(3)(5)(8) E.(1)(2)(8) F.(2)(3)(5)G.(5)(6)(8)H.(4)(7)I.全部正确J.J:全部错误
答案
幂级数的收敛半径和收敛域( )/ananas/latex/p/250868
答案
幂级数的收敛域不可能是
答案
幂级数的收敛半径为2,则幂级数的收敛区间是()
A.(-2,2) B.(-2,4) C.(0,4) D.(-4,0)
答案
热门试题
设 收敛,则级数 ( ).
设幂级数 和 的收敛半径分别为 ,则和级数 = + 的收敛半径 .
设幂级数和的收敛半径分别为,则和级数=+的收敛半径()
将f(x)=1/(2-x)展开为x的幂级数,其收敛域为( )。
设x=-1的时候,级数?条件收敛,则级数?
如果级数在收敛,那么对满足的,级数必绝对收敛。
已知的收敛域为()。
已知的收敛半径R=1,的收敛域为()
若的收敛域是(-8,8],则的收敛域分别是()
已知级数与广义积分均收敛,则p的取值范围是()
已知级数与广义积分均收敛,则p的取值范围是()
将f(x)=ln(4x-5)展开成x-2的幂级数,并指出其收敛域.
下列级数中,条件收敛的级数是( ).
正项级数有上界是该级数收敛的()
若数项级数收敛
下列级数收敛的是()
已知序列Z变换的收敛域为|z|>1,则该序列为()
下列级数中收敛的是()
下列级数中收敛的是()
下列级数绝对收敛的是()



 使用微信扫一扫登录
使用微信扫一扫登录