设f(x)具有任意阶导数,且f′(x)=[f(x)]2,则f(n)(x)=( )。
A. n[f(x)]n+1
B. n![f(x)]n+1
C. (n+1)[f(x)]n+1
D. (n+1)![f(x)]n+1
查看答案
相关试题
换一换


设f(x)具有任意阶导数,且f′(x)=[f(x)]2,则f(n)(x)=( )。
A.n[f(x)]n+1 B.n![f(x)]n+1 C.(n+1)[f(x)]n+1 D.(n+1)![f(x)]n+1
答案
设f具有一阶连续导数,且y=ef(2sinx),则y′=().
答案
设z=f(x2+y2),其中f具有二阶导数,则等于().
答案
设f(x),g(x)具有任意阶导数,且满足f″(x)+f′(x)g(x)+f(x)x=ex-1,f(0)=1,f′(0)=0。则( )。
A.f(0)=1为f(x)的极小值 B.f(0)=1为f(x)的极大值 C.(0,f(0))为曲线y=f(x)的拐点 D.由g(x)才能确定f(x)的极值或拐点
答案
设偶函数f(x)具有二阶连续导数,且f″(0)≠0,则x=0( )。
A.一定不是函数的驻点 B.一定是函数的极值点 C.一定不是函数的极值点 D.不能确定是否为函数的极值点
答案
设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为____。
答案
设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。
A.f″(x)+f(x)=0 B.f′(x)+f(x)=0 C.f″(x)+f′(x)=0 D.f″(x)+f′(x)+f(x)=0
答案
设y=In(sinx) , 则=阶导数y"等于()
A. B.
B.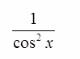 C.
C.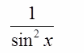 D.
D.
 B.
B.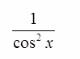 C.
C.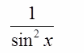 D.
D.
答案
如果函数在具有任意阶导数,则存在,使得在可以展开成泰勒级数.( )
答案
0303 解析函数在其解析区域内具有任意阶导数。
答案
热门试题
设函数f(x)在点x=O的某邻域内具有连续的二阶导数,且f′(0)=f″(0)=0,则( )。
设z=f(x,xy)二阶偏导数连续,则∂2z/∂x∂y=____。
设A为3阶矩阵,且|A|=2,则|2A|=
函数厂(x)具有连续的二阶导数,且f″(0)≠0,则x=0( )。《》( )
函数f(x)具有连续的二阶导数,且f″(0)≠0,则x=0()
设A为三阶矩阵,且|A|=-2,则
设z=f(xy)/x+yφ(x+y),f、φ具有二阶连续导数,则∂2z/∂x∂y=____。
设f有二阶偏导数,z=f(xy),则∂2z/∂x∂y等于( )。
设z=f(x,y),φ(x,y)=0,其中f和φ对x、y具有二阶连续偏导数且φy′≠0,求z对x的二阶导数。
设则f (x)在x=0时的6阶导数是()。
设z=f(xy)/x+yφ(x+y),f和φ具有二阶连续导数,则∂2z/∂x∂y=____。
设A为4阶矩阵,且|A|=-3,则|2A|=______.
设y=f(x)在(a,6)内有二阶导数,且,f″>0,则曲线y=f(x)在(a,6)内().
设z=f(x2-y2,exy),其中f具有连续二阶偏导数,求∂z/∂x,∂z/∂y。
设f(x)的二阶导数存在,且f′(x)=f(1-x),则下列式中何式可成立()?
设f(x)的二阶导数存在,且f′(x)=f(1-x),则下列式中何式可成立()?
称二阶导数的导数为三阶导数,阶导数的导数为阶导数。()
设 A 为 n 阶方阵,且|A|=3,则|2A|=6.
设u=f(x+y,xz)有二阶连续偏导数,则∂2u/∂x∂z=( )。
设A为n阶方阵,E为n阶单位矩阵,且A2=A,则(A-2E)-1=____。



 使用微信扫一扫登录
使用微信扫一扫登录