设f(x)在[a,b]上连续,在(a,b)内可微,若a≥0,证明在(a,b)内存在三个数x1、x2、x3,使f′(x1)=(b+a)f′(x2)/(2x2)=(b2+ab+a2)f′(x3)/(3x32)。
查看答案
相关试题
换一换


设a>0,b>0,证明:ab+ba>1
答案
设f(x)在[a,b]上连续,在(a,b)内可微,若a≥0,证明在(a,b)内存在三个数x1、x2、x3,使f′(x1)=(b+a)f′(x2)/(2x2)=(b2+ab+a2)f′(x3)/(3x32)。
答案
设AB为门阶方阵,若AB等价,则AB相似()
答案
设AB为门阶方阵,若AB等价,则AB相似
答案
设f(x)在[0,π]上连续,在(0,π)内可导,证明:必∃ξ∈(0,π),使f′(ξ)+3f(ξ)cotξ=0。
答案
若a<b<0,则ab<0。()
答案
设A、B都是n阶方阵,满足AB=A-B,请证明:AB=BA
答案
设y=f(x)在[a,b]上连续,在(a,b)内可导,若存在唯一点x0∈(ab),使f′(x0)=0,且在x0左右两侧f′(x)异号,则点x=x0必为f(x)的()
A.极值点且为最值点 B.极值点但不是最值点 C.最值点但非极值点 D.以上都不对
答案
设A,B是n阶方阵,A≠0且AB=0,则( ).
A.|B|=0或|A|=0: B.B=0; C.BA=O: D.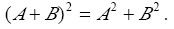
答案
设A,B是n阶方阵,A≠0且AB=0,则( ).
A.| B.B=0; C.BA=O: D.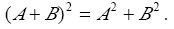
答案
热门试题
设A为n阶方阵,若对任意n×m(m≥n)矩阵B都有AB=0,则A=____。
设A,B都是N阶对称矩阵,证明AB是对称矩阵的充分必要条件是.AB=BA
设A,B都是n阶对称阵,证明AB是对称阵的充要条件是AB=BA.
设甲:a>0且b>0;乙:ab>0,则甲是乙的( )
若点A(0,3),B(-4,0),则|AB|=( )。
设矩阵A,B,C,若AB=AC,则B=C
因为A+AB=A,所以AB=0
设函数f(x)在[a,b]上连续,在(a,b)内可导,f′(x)>0.若f(a)·f(b)<0,则y=f(x)在
(a,b)内()
设f(x)在[a,b]上连续(a>0),在(a,b)内可导,证明:必∃ξ∈(a,b),使[f(a)-f(ξ)]/(ξ2-b2)=f′(ξ)/(2ξ)。
若事件A、同时出现的概率P(AB)=0,则( )。
在门电路中,若A=1,B=0,则AB=()。
若16a+98b=0,则ab是:
设A与B都是n阶正交矩阵,证明AB也是正交矩阵.
设3阶矩阵A,B满足AB=A+B.证明A-E可逆.
设A(1,2,3),B(-1,2,0),C(1,1,1)则AB(→)·BC(→)=____,AB(→)×BC(→)=____,△ABC的面积=____。
对于任意两事件A和B,若P(AB)=0,则( )。
若事件A、B同时出现的概率P(AB)=0,则( )。
若P(AB)=0,则A、B一定是互斥的
设函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),证明:若f(x)不恒为常数,则至少存在一点ξ∈(a,b),使得f′(ξ)>0.
设f(x)在[a,+∞)上连续,在(a,+∞)内可导,且f′(x)>k>0(k为常数),又f(a)<0,证明方程f(x)=0在(a,a-f(a)/k)内有唯一实根。



 使用微信扫一扫登录
使用微信扫一扫登录