过圆x2+y2=25上一点M(-3,4)作该圆的切线,则此切线方程为
查看答案
相关试题
换一换


过圆x2+y2=25上一点M(-3,4)作该圆的切线,则此切线方程为
答案
过圆x2+y2=25 上一点 P(3,4)的切线方程为()
A.3x+4y-25 =0 B.3x+4y+25 =0 C.3x-4y-25=0 D.3x-4y+25=0
答案
由直线y=x+1上的一点向圆(x-3)²+y²=1引切线,则切线长的最小值为( ).
A.1 B.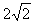 C.
C.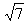 D.3
D.3
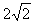 C.
C.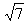 D.3
D.3 答案
从点M(x,3)向圆(x+2)2+(y+2)2=1作切线,切线长的最小值等于( )。
A.4 B.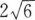 C.5 D.
C.5 D.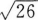
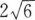 C.5 D.
C.5 D.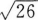
答案
已知圆x2+y2+4x-8y+11=0,经过点P(1,0)作该圆的切线,切点为Q,则线段PQ的长为( )
A.10 B.4 C.16 D.8
答案
过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答案
已知曲线y=x3-3x2-1,过点(1,-3)作其切线,求切线方程。
答案
已知圆22+y2+4x-8y+11=0,经过点P(1,o)作该圆的切线,切点为Q,则线段PQ的长为 ( )
A.10 B.4 C.16 D.8
答案
设曲线y=f(x)和y=x2-x在点(1,0)处有相同的切线,则f(x)在该点处的切线斜率为().
答案
设曲线y=x2+x-2在点M处切线的斜率为2,则点M的坐标为().
答案
热门试题
过曲线y=(x-1)2上一点(-1,4)的切线斜率为()。
已知直线l是圆x2+y2=5在点(1,2)处的切线,则l在y轴上的截距为
设曲线y=f(x)在点(1,f(1))处的切线平行于x轴,则该切线方程()。
已知圆C,x2+(y-a)2=b若圆C在点(1,2)处的切线与Y轴及点为(0.3)则ab=
若3x-y+4=0与6x-2y-1=0是圆的两条平行切线,则此圆的面积为( )
一曲线在其上任一点的切线的斜率为-2x/y,则此曲线是( )。
在曲线x=t,y=t2,z=t3上某点的切线平行于平面x+2y+z=4,则该点的坐标为:()
曲线y=2x2+3x−26在点M处的切线斜率是15,则点M的坐标是( ).
已知一曲线y=y(x)通过原点,且曲线上任意一点(x,y)处的切线斜率均等于2x+y,求该曲线方程.
若y=x2与y=x3在某点处的切线平行,则该点的横坐标为x=().
曲线y=2x2在点(1,2)处有切线,曲线的切线方程为y=()。
由点P(1,3)引圆x2+y2=9的切线的长是()
圆X2+y2=5在点(1,2)处切线的方程为()。
设曲线y=cos2x+aex+1在点x=0处的切线与直线y=2x-3平行,求该切线方程。
曲线y=2x2+3x-26上点M处的切线斜率是15,则点M的坐标是().
求曲线y=x2在点(a,a2)(a<1)的一条切线,使由该切线与x=0、x=1和y=x2所围图形的面积最小。
曲线y=f(x)上任一点(x,y)处的切线斜率为4x3+cos(x-1),且过点(1,1),则该曲线方程是
()
曲线y=x3+2x-1在点M(1,2)处的切线方程是
圆x2+y2=5在点(1,2)处的切线的方程为()。
设曲线y=ax2+2x在点(1,a+2)处的切线与y=4x平行,则a=______.



 使用微信扫一扫登录
使用微信扫一扫登录