过圆x2+y2=25 上一点 P(3,4)的切线方程为()
A. 3x+4y-25 =0
B. 3x+4y+25 =0
C. 3x-4y-25=0
D. 3x-4y+25=0
查看答案
相关试题
换一换


过圆x2+y2=25 上一点 P(3,4)的切线方程为()
A.3x+4y-25 =0 B.3x+4y+25 =0 C.3x-4y-25=0 D.3x-4y+25=0
答案
过圆x2+y2=25上一点M(-3,4)作该圆的切线,则此切线方程为
答案
设y(x)是区间(0,3/2)内的可导函数,且y(1)=0,点P是曲线L:y=y(x)上的任意一点,L在点P处的切线与y轴相交于点(0,yp),法线与x轴相交于点(xp,0),若xp=yp,求L上点的坐标(x,y)满足的方程。
答案
已知一曲线y=y(x)通过原点,且曲线上任意一点(x,y)处的切线斜率均等于2x+y,求该曲线方程.
答案
经过点(2,10),且在没一点的切线斜率都为3x的曲线方程式y=3/2x^2+4()
答案
曲线y=2x2在点(1,2)处的切线方程y=______.
答案
曲线y=2x2在点(1,2)处有切线,曲线的切线方程为y=()。
答案
设曲线y=y(x)上点P(0,4)处的切线垂直于直线x-2y+5=0,且该点满足微分方程y″+2y′+y=0,则此曲线方程为( )。
A.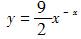 B.
B.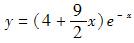 C.
C.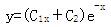 D.
D.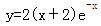
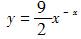 B.
B.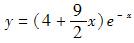 C.
C.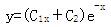 D.
D.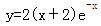
答案
曲线y=2x2在点(1,2)处的切线方程y=______。
答案
过曲线y=(x-1)2上一点(-1,4)的切线斜率为()。
A.-4 B.0 C.2 D.-2
答案
热门试题
已知曲线y=x3-3x2-1,过点(1,-3)作其切线,求切线方程。
曲线y=x^2+x-2在点(1.5,1.75)处的切线方程为()
曲线y=x+sin2x在点(π/2,1+π/2)处的切线方程是____。
曲线y=2x2在点(1,2)处的切线方程为y=()。
曲线y=2x2在点(1,2)处的切线方程为y=().
曲线y=x+sin^2x在点(π/2,1+π/2)处的切线方程是( )。
曲线x2+y2=2x在点(1,1)处的切线方程为.
曲线y=x3-4x+2在点(1,-l)处的切线方程为()
曲线y=x4-3在点(1,-2)处的切线方程为()
曲线y=x3+2x-1在点M(1,2)处的切线方程是
求曲线y=e-x上通过原点的切线方程及与直线x+y=2垂直的法线方程.
曲线y=x3-2x在点(1,-1)处的切线方程为______.
曲线y=x3—2x在点(1,-1)处的切线方程为 .
曲线y=x3-x在点(1,0)处的切线方程y=______.
曲线y=x2+3x+4在点(-1,2)处的切线方程为______
曲线:y=x2+3x+4在点(-1,2)处的切线方程为
曲线y=f(x)上任一点(x,y)处的切线斜率为4x3+cos(x-1),且过点(1,1),则该曲线方程是
()
已知О为坐标原点,抛物线C:y²= 2px(p >0)的焦点为F ,P为C上一点,PF与x轴垂直,Q为x上一点,且PQ⊥OP ,若|FQ|=6,则C的准线方程为_____
设曲线y=cos2x+aex+1在点x=0处的切线与直线y=2x-3平行,求该切线方程。
求曲线y=x2在点(1,1)处的切线方程。



 使用微信扫一扫登录
使用微信扫一扫登录