2024年成考高起点每日一练《数学(理)》8月22日

• 1. 设A、B、C是三个随机事件,用A、B、C的运算关系（）表示事件:B、C都发生,而A不发生  

  A

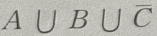
  B

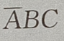
  C

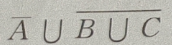
  D

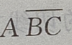
• 2. 分别和两条异面直线AB、CD同时相交的两条直线AC、BD（）。

  A相交

  B平行

  C是异面直线

  D垂直

• 3. 设f(x)=x³+ax²+x为奇函数，则a=（）。

  A1

  B0

  C

  D-2 D.C.-1

• 4. 已知向量a=(3,4),向量 b=(0,-2),则cos的值为（）

  A

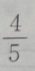
  B

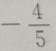
  C

  D

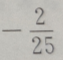
• 1. 设分别讨论x→0及x→1时f（x）的极限是否存在？

• 2. 已知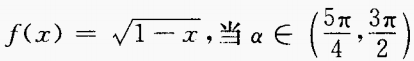时，化简式子f(sin2α)-f(- sin2α)。

• 3. 已知数列{a_n}中，a₁=2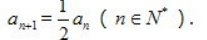， （Ⅰ）求数列{a_n}的通项公式; （Ⅱ）求数列{a_n}前5项的和 S₅

• 4. 求下列函数的定义域： （1）
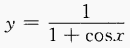
  （2）
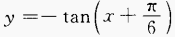
  （3）  

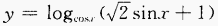
• 1. =______。  

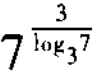• 2. cos²67.5°- 0.5=______。