2017上半年教师资格证考试《初中数学》真题及答案

• 1.

• 2. 下列矩阵所对应的线性变换为关于y=-x的对称变换的是()。

• 3.

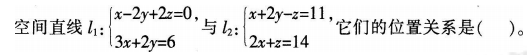
  Aι1与ι2垂直

  Bι1与ι2相交，但不一定垂直

  Cι1与ι2为异面直线

  Dι1与ι2平行

• 4.

  A对任意x∈[a，b]，都有f(x)=0

  B至少存在一个x∈[a，b]使f(x)=0

  C对任意x∈[a，b]，都有f(x)≠0

  D不一定存在x∈[a，b]使f(x)=0

• 5.

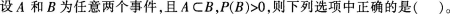
  AP(B)

  BP(A)≤P(A|B)

  CP(B)>P(A|B)

  DP(A)≥P(A|B)

• 6.

  A(0，1)T

  B(1，2)T

  C(-1，1)T

  D(1，0)T

• 7. 与意大利传教士利玛窦共同翻译了《几何原本》(I—Ⅵ卷)的我国数学家是()。

  A徐光启

  B刘徽

  C祖冲之

  D杨辉

• 8. 在角、等边三角形、矩形和双曲线四个图形中，既是轴对称又是中心对称的图形有()。

  A1个

  B2个

  C3个

  D4个

• 1. 已知抛物面方程2x2+y2=z。(1)求抛物面上点M(1，1，3)处的切平面方程；
  (2)当k为何值时，所求切平面与平面3x+ky-4z=0相互垂直。

• 2. 已知向量组a1=(2，1，-2)，a2=(1，1，0)，a3=(t，2，2)线性相关。(1)求t的值；
  (2)求出向量组{a1，a2，a3}的一个极大线性无关组。

• 3. 有甲、乙两种品牌的某种饮料，其颜色、气味及味道都极为相似，将饮料放在外观相同的6个杯子中，每种品牌各3杯，作为试验样品。(1)从6杯样品饮料中随机选取3杯作为一次试验，若所选饮料全部为甲种品牌，视为成功。独立进行5次试验，求3次成功的概率；
  (2)某人声称他通过品尝饮料能够区分这两种品牌。现请他品尝试验样品中的6杯饮料进行品牌区分，作为一次试验，若区分完全正确，视为试验成功。他经过5次试验，有3次成功，可否由此推断此人具有品尝区分能力?说明理由。

• 4. 《义务教育数学课程标准(2011年版)》用行为动词“了解”“理解”“掌握”“应用”等描述结果目标，请解释“了解等腰三角形的概念”的具体含义。

• 5. 书面测验是考查学生课程目标达成状况的重要方式，以“有理数”一章为例，说明设计数学书面测验试卷应关注的主要问题。

• 1. 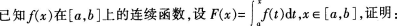(1)F(x)在[a，b]上连续；(2)F(x)在[a，b]上可导，

• 1. 推理一般包括合情推理与演绎推理。(1)请分别阐述合情推理与演绎推理的含义；
  (2)举例说明合情推理与演绎推理在解决数学问题中的作用，并阐述二者间的关系。

• 1. 案例：为了帮助学生理解正方形的概念、性质，发展学生推理能力、几何直观能力等，一节习题课上，甲乙两位教师各设计了一道典型例题。
  【教师甲】
  如图1，在边长a的正方形ABCD中，E为AD边上一点(不同于A，D)，连CE，在该正方形边上选取点F，连接DF，使DF=CE。
  请解答下面的问题：
  (1)满足条件的线段DF有几条?
  (2)根据(1)的结论，分别判断DF与CE的位置关系，并加以证明。
  
  
  【教师乙】
  如图2，在边长为a的正方形ABCD中，E，F分别为AD，AB边上的点(点E，F均不与正方形顶点重合)，且AE=BF，CE，DF相交于点M。
  证明：
  (1)DF=CE；(2)DF⊥CE。
  
  
  问题：
  (1)分析两位教师例题设计的各自特点。
  (2)直接写出教师甲的例题中两个问题的结论(不必证明)。
  (3)结合两位教师设计的例题，你还能启发学生提出哪些数学问题?(请写出至少两个问题)。

• 1. 针对一元二次方程概念与解法的一节复习课，教学目标如下：①进一步了解一元二次方程的概念；
  ②进一步理解一元二次方程的多种解法(配方法、公式法、因式分解法等)；
  ③会运用判别式判断一元二次方程根的情况：
  ④通过对相关问题的讨论，在理解相关知识的同时，体会数学思想方法，积累数学活动经验。
  问题：
  根据上述教学目标，完成下列任务：
  (1)为了落实上述教学目标①、②，请设计一个教学片段，并说明设计意图；
  (2)配方法是解一元二次方程的通性通法，请设计问题串，以帮助学生进一步理解配方法在解一元二次方程中的作用。