高中数学学科知识与教学能力试题(二)

• 1. 设区域D={(x，y)|x2+y2≤4}，则()。

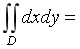  A8π

  B2π

  C16π

  D4π

• 2. 对于函数的教学以下说法不正确的是（） 

  A对函数的学习不能停留在抽象的讨论，要突出函数图形的地位

  B函数是最重要、最基本的数学模型，要加深对函数思想的理解与应用

  C在学生头脑中留下几个具体的最基本的函数模型就可以了

  D结合具体的数学内容采用多种模式，让学生经历函数知识的形式与应用过程

• 3. 在由数字1，2，3，4，5组成的所有没有重复数字的五位数中，大于23145且小于43521的数共有（）

  A56个

  B57个

  C58个

  D60个

• 4. 《几何原本》传入中国，首先应归功于科学家()。

  A刘徽

  B秦九韶

  C徐光启

  D李善兰

• 5. 在学习数学和应用数学的过程中逐步形成和发展的数学学科核心素养包括：()、直观想象、数学运算、数据分析等。

  A分类讨论

  B数学建模

  C数形结合

  D分离变量

• 6. 已知三点A(1，2，3)，B(3，4，5)，C(2，4，7)，则△ABC的面积为()。

  A14

  B5

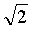
  C2

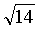
  D

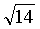
• 7. 在空间直角坐标系下，过点(2，1，-3)，且以n=(1，-2，3)为法向量的平面方程是()。

  A2x+y-3z-9=0

  B2x+y-3z+9=0

  Cx-2y+3z-9=0

  Dx-2y+3z+9=0

• 8. 已知2n阶行列式D的某一列元素及其余子式都等于a，则D等于（）。

  A1

  B0

  Ca2

  D-a2

• 1. 求曲面x2+2y2+3z2=21的切平面，使它平行于平面x+4y+6z=0。

• 2. 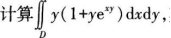其中平面区域D由直线y=x，y=-1及x=1所围成。

• 3. 用几何方法证明当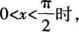sinx

• 4. 高中数学课程为什么要加入“微积分初步”?

• 5. 合情推理包括归纳推理和类比推理，请举例说明归纳推理和类比推理在数学教学中的运用，并简述二者之间的关系。

• 1.

• 1. 通过各种载体增强学生的数学应用意识，可以有效地激发学生将数学知识应用于实践的积极性，提高他们利用数学知识解决问题的能力。函数作为一种重要的数学模型，用函数模型解决实际问题需要建立的函数模型是多种多样的，请简要介绍解决函数应用问题时的过程。

• 1. 案例：在求解题目“已知双曲线的右准线为x=4，右焦点F(10，0)，离心率e=2，求双曲线方程。”两位同学解题方法如下：
  
  问题：
  (1)指出学生的错误之处；
  (2)分析学生的错误原因；
  (3)写出正确解法。
  "

• 1. 通过直观感知、操作确认，归纳出平面与平面平行的判定定理：如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行。请完成下列任务：
  (1)写出本节课的教学目标和教学重点；
  (2)请设计一个引入新课的问题情境以展开新课的教学，并说明设计意图；
  (3)请设计一个探索活动来探究该定理；
  (4)请你设计两道习题(不必解答)，进一步帮助学生理解并应用该定理，并说明设计意图。