2017上半年教师资格证考试《高中数学》真题及答案

• 1.

  A

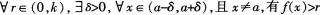
  B

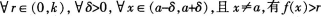
  C

  D

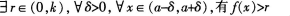
• 2. 下列矩阵所对应的线性变换为旋转变换的是( )。

  A

  B

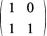
  C

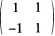
  D

• 3.

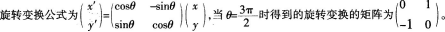
  A

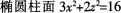
  B

  C

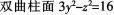
  D

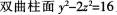
• 4. 若f(x)是连续函数，则下列命题不正确的是( )。

  A

  Bf(x)有无穷多个原函数

  C

  D

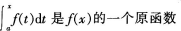
• 5.

  AP(B)

  BP(A)≤P(AB)

  CP(B)>P(AB)

  DP(A)≥P(AB)

• 6.

  A

  B(2，0，1)T

  C(-1，0，1)T

  D(0，0，1)T

• 7. 与意大利传教士利玛窦共同翻译了《几何原本》(I-Ⅵ卷)的我国数学家是（ ）

  A徐光启

  B刘徽

  C祖冲之

  D杨辉

• 8. “有一个角是直角的平行四边形是矩形”，这个定义方式属于( )。

  A公理定义

  B属加种差定义

  C递归定义

  D外延定义

• 1. 已知椭球面方程2x2+y2+3z2=6。
  (1)求椭球面上点M(1，1，1)处的切平面方程；
  (2)当k为何值时，所求的切平面与平面5x+ky-4z=0相互垂直。

• 2. 已知向量组a1=(2，1，-2)，a2=(1，1，0)，a3=(t，2，2)线性相关。
  (1)求t的值；
  (2)求出该向量组的一个极大线性无关组，并将其余向量用极大无关组线性表示。

• 3. 有甲、乙两种品牌的某种饮料，其颜色、气味及味道都极为相似，将饮料放在外观相同的6个杯子中，每种品牌各3杯，作为试验样品。
  (1)从6杯样品饮料中随机选取3杯作为一次试验，若所选饮料全部为甲种品牌，视为成功。独立进行5次试验，求3次成功的概率；
  (2)某人声称他通过品尝饮料能够区分这两种品牌。现请他品尝试验样品中的6杯饮料进行品牌区分，作为一次试验。若区分完全正确，视为试验成功。他经过5次试验，有3次成功，可否由此推断此人具有品尝区分能力?说明理由。

• 4. 《普通高中数学课程标准(实验)》用行为动词“了解”“理解”“掌握”“应用”等描述知识与技能目标，请解释“了解函数奇偶性”的具体含义。

• 5. 书面测验是考查学生课程目标达成状况的重要方式，以“数列”一章为例，说明设计数学书面测验试卷应关注的主要问题。

• 1.
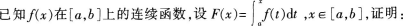
  (1)F(x)在[a，b]上连续；(5分)
  (2)F(x)在[a，b]上可导，且F´(x)=ƒ(x)。

• 1. 推理一般包括合情推理与演绎推理。
  (1)请分别阐述合情推理与演绎推理的含义；
  (2)举例说明合情推理与演绎推理在解决数学问题中的作用，并阐述二者间的关系。

• 1. 案例：
  在学习《平面向量》后，某数学教师安排了如下一道选择题：
  若非零向量a，b满足|a-b|=|b|，则( )。 A．|2b|>|a-2b|
  B．|2b|<|a-2b|
  C．|2a|>|2a-b|
  D．|2a|<|2a-b|
  教师要求学生写出他们详细的解题过程，三位学生分别给出了如下的解法：
  学生1：因为|a-b|=|b|，所以a-b=b或a-b=-b，故a=2b或a=0(舍去)，所以|a-2b|=0。由于b是非零向量，所以|2b|>0，故|2b|>|a-2b|，选A。
  学生2：因为|a-b|=|b|，所以(a-b)(a-b)=b·b，a·a-2a·b+b·b=b·b，所以a·a=2a·b，所以a=2b，故|a-2b|=0。由于b是非零向量，所以|2b|>0，故|2b|>|a-2b|，选A。
  学生3：因为|a-b|=|b|，所以|a-b|²=|b|²，|a|²-2|a||b|+|b|²=|b|²，|a|²=2|a||b|，所以|a|=2|b|，故|a-2b|=0。由于b是非零向量，所以|2b|>0，故|2b|>|a-2b|，选A。
  问题：
  (1)如果你是这位数学教师，请指出这三种解法存在的错误；
  (2)请你从已知条件|a-b|=|b|出发，通过数形结合，引导学生给出一种正确的解法；
  (3)针对学生在向量运算中的错误，请写出实数运算与向量运算的不同点(至少写出三点)。
  
  

• 1. 单调性是函数的基本性质之一。针对高中函数单调性中“增(减)函数”概念的教学，请完成下面的任务：
  (1)给出“增(减)函数”概念形成过程中教学的重、难点；
  (2)说明“增(减)函数”定义的要点；
  (3)根据(2)中“增(减)函数”定义的要点，请写出教学设计思路。