相关试题
换一换


罗尔中值定理告诉我们:可导函数在区间内取得极值点处的切线斜率为零()
A.正确 B.错误
答案
下列函数在指定区间上满足罗尔中值定理条件的是()。
A.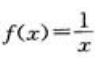 ,x∈[2,0] B.f(x)=(x-4)2,x∈[-2,4] C.f(x)=sinx,
,x∈[2,0] B.f(x)=(x-4)2,x∈[-2,4] C.f(x)=sinx,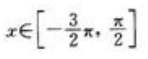 D.f(x)=|x|,x∈[-1,1]
D.f(x)=|x|,x∈[-1,1]
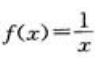 ,x∈[2,0] B.f(x)=(x-4)2,x∈[-2,4] C.f(x)=sinx,
,x∈[2,0] B.f(x)=(x-4)2,x∈[-2,4] C.f(x)=sinx,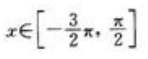 D.f(x)=|x|,x∈[-1,1]
D.f(x)=|x|,x∈[-1,1] 答案
下列函数在给定区间上满足罗尔中值定理条件的是()
A.y= ,[-1,1] B.y=xe-x,[-1,1] C.y=
,[-1,1] B.y=xe-x,[-1,1] C.y=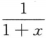 ,[-1,1] D.y=lnx2,[-1,1]
,[-1,1] D.y=lnx2,[-1,1]
 ,[-1,1] B.y=xe-x,[-1,1] C.y=
,[-1,1] B.y=xe-x,[-1,1] C.y=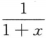 ,[-1,1] D.y=lnx2,[-1,1]
,[-1,1] D.y=lnx2,[-1,1] 答案
在区间[-1,1]上,下列函数不满足罗尔中值定理条件的是()
A.f(x)= -1 B.f(x)=ln(1+x2) C.f(x)=
-1 B.f(x)=ln(1+x2) C.f(x)=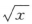 D.f(x)=
D.f(x)=
 -1 B.f(x)=ln(1+x2) C.f(x)=
-1 B.f(x)=ln(1+x2) C.f(x)=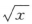 D.f(x)=
D.f(x)=
答案
下列函数中,在区间[-1,1]上不满足罗尔中值定理条件的是()。
A.f(x)=sin2x B. C. f(x)=In|x| D.
C. f(x)=In|x| D.
 C. f(x)=In|x| D.
C. f(x)=In|x| D.
答案
使函数 满足罗尔定理的区间是( )。
答案
设函数在可导,取定,在区间上用拉格朗日中值定理,有,使得,这里的是的函数()
A.正确 B.错误
答案
罗尔中值定理是拉格朗日中值定理的特殊情况。()
A.错误 B.正确
答案
函数 在区间 上是否满足罗尔定理的条件?_
答案
试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,(a)),(b,(b)),(x,(x)))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理。
答案
热门试题
试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,ƒ(a)),(b,ƒ(b)),(x,ƒ(x))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理。
罗尔定理:设函数ƒ(x)满足条件:(1)在闭区间[a,b]上连续,(2)在开区间(a,b)内可导,(3)ƒ(a)=ƒ(b),则在(a,b)内至少存在一点ξ,使得ƒ´(ξ)=0。证明这个定理并说明其几何意义。
罗尔定理条件:要求函数在闭区间a.b内连续,(),端点的函数值相等
下列函数在区间[-1,1]上满足罗尔定理条件的是( )。
(拉格朗日中值定理)下列函数在区间[-1,1]上满足拉格朗日中值定理条件的是
在区间[-2,2]上,下列函数中不满足罗尔定理条件的是()。
“罗森塔尔效应”告诉我们要多给学生以鼓励,要看到学生行为中的闪光点。
“罗森塔尔效应”告诉我们要多给学生以鼓励,要看到学生行为中的闪光点。
可导函数f(x)的极值点一定是f(x)的驻点
如果f(x)=x2+kx+3在区间[-1,3]上满足罗尔中值定理的条件,则k=().
函数在取得极值的点处偏导数一定存在。
下列函数在给定区间上满足拉格朗日中值定理条件的是()
莱布尼兹公式告诉我们:如果函数f(x)在[a,b]上连续,且存在原函数,那么f在区间[a,b]上一定可积。()
心理学中的罗森塔尔效应告诉我们在教育活动过程中要
对于函数f(x)=[(x^2-1)(x^2-4)]^(2/3),下列能满足罗尔定理条件的区间是()
生产函数可以告诉我们的是,企业()
函数在点处是否可导?为什么?
只要函数值在区间端点处异号,则该函数在区间内肯定存在零点()
下列函数在[-1,1]上满足罗尔定理条件的是
下列函数在[-1,1]上满足罗尔定理条件的是()。



 使用微信扫一扫登录
使用微信扫一扫登录